0 50970 50978 50984 50988 50994 50996 51000 51006 51008 51014 51020 51024 51026 51030 51036 51038 51044 51048 51050 51054 51056 51060 51062 51064 51065 51066 51068 51069 51070 51072 51074 51078 51080 51084 51086 51090 51096 51098 51104 51108 51110 51114 51120 51126 51128 51134 51138 51140 51146 51150 51156 51164 447348
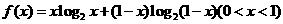 ,求
,求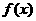 的最小值;
的最小值;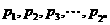 满足
满足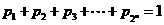 ,
,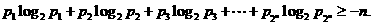
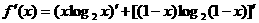
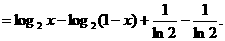
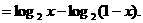
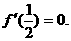
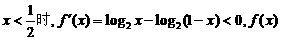 在区间
在区间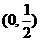 是减函数,
是减函数,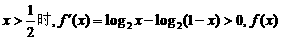 在区间
在区间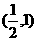 是增函数.
是增函数.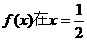 时取得最小值,
时取得最小值,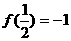 ,
,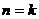 时命题成立,即若正数
时命题成立,即若正数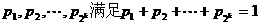 ,
,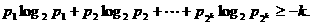
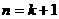 时,若正数
时,若正数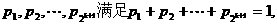
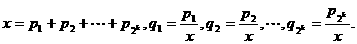
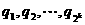 为正数,且
为正数,且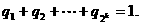
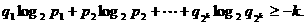
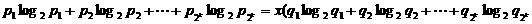
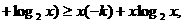 ①
①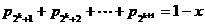 可得
可得
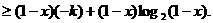 ②
②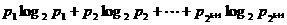
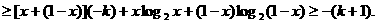
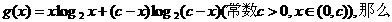
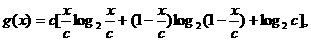
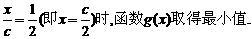
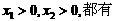
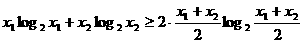
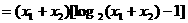 . ①
. ①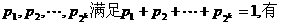
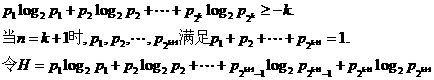
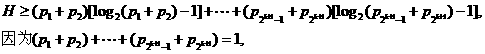
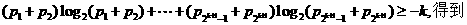
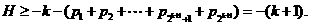
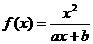 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.(1)求函数f(x)的解析式;
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.(1)求函数f(x)的解析式;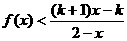 .
.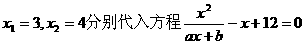 得
得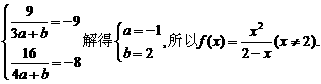
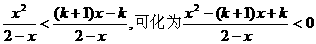
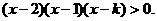
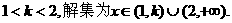
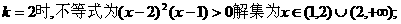
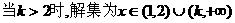 .
.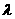 f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数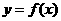 的图象上任一点
的图象上任一点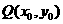 关于原点的对称点为
关于原点的对称点为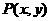 ,
,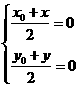 即
即 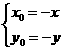 .
.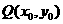 在函数
在函数
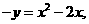 即
即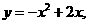 故g(x)=
故g(x)=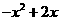 .
.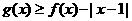 可得:
可得: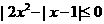
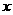
 1时,
1时,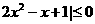
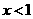 时,
时,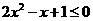

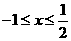
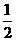 ].
].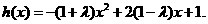
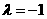 时,
时,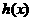 =
=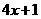 在[-1,1]上是增函数,
在[-1,1]上是增函数,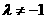 时,对称轴的方程为
时,对称轴的方程为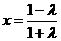
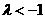 时,
时,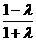
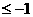 ,解得
,解得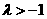 时,
时,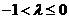
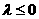
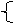 .[解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)
.[解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)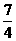 )2+
)2+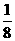
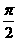
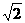 sinx, α=π,
sinx, α=π, (0, x2),则x1<x2<x*,从而f(x*)≥f(x2)>f(x1),
(0, x2),则x1<x2<x*,从而f(x*)≥f(x2)>f(x1),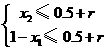 ①
①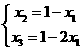 ,
,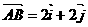 (
(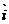 、
、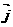 分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.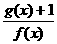 的最小值.
的最小值.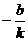 ,0),B(0,b),则
,0),B(0,b),则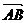 ={
={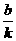 ,b},于是
,b},于是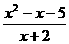 =x+2+
=x+2+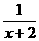 -5
-5 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg ,且不等式
,且不等式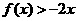 的解集为
的解集为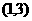 。(Ⅰ)若方程
。(Ⅰ)若方程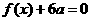 有两个相等的根,求
有两个相等的根,求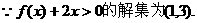
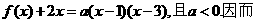
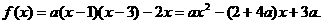 ①
①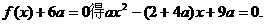 ②
②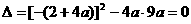 ,
,
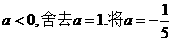 代入①得
代入①得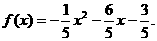
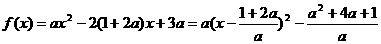

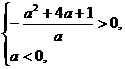 解得
解得 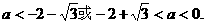
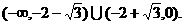
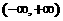 上满足
上满足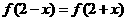 ,
,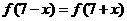 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有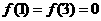 .
.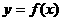 的对称轴为
的对称轴为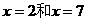 ,
,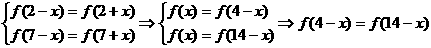
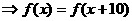 ,从而知函数
,从而知函数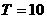
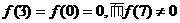 ,故函数
,故函数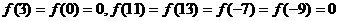
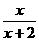 (x∈R,且x≠-2)的反函数是
(x∈R,且x≠-2)的反函数是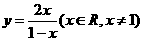 .
.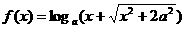 是奇函数,则a=
.
是奇函数,则a=
.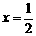 对称,则f (1)+ f (2)+ f (3)+ f
(4)+ f (5)=_0_______________.
对称,则f (1)+ f (2)+ f (3)+ f
(4)+ f (5)=_0_______________.