0 50935 50943 50949 50953 50959 50961 50965 50971 50973 50979 50985 50989 50991 50995 51001 51003 51009 51013 51015 51019 51021 51025 51027 51029 51030 51031 51033 51034 51035 51037 51039 51043 51045 51049 51051 51055 51061 51063 51069 51073 51075 51079 51085 51091 51093 51099 51103 51105 51111 51115 51121 51129 447348
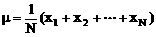 为总体平均数(μ为N个个体的算术平均数)
为总体平均数(μ为N个个体的算术平均数)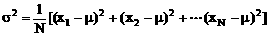 ,则称
,则称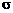 2为总体方差,
2为总体方差,
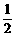 ,tanβ=
,tanβ=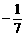 ,α,β∈(-π,0),求2α-β的值。
,α,β∈(-π,0),求2α-β的值。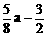 在闭区间[0,
在闭区间[0,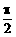 ]上的最大值是1?若存在,求出对应的a值。
]上的最大值是1?若存在,求出对应的a值。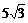 cos2x+
cos2x+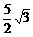 (x∈R)
(x∈R)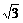 cos(x-θ)的图象关于y轴对称,则θ=________。
cos(x-θ)的图象关于y轴对称,则θ=________。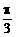 ,且
,且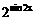
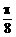 对称,则a值为
对称,则a值为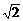 B、-1 C、1
D、
B、-1 C、1
D、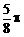 时,ymin=-2,则此函数解析式为
时,ymin=-2,则此函数解析式为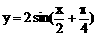 B、
B、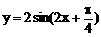 C、
C、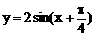 D、
D、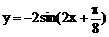
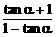 =1998,则
=1998,则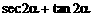 的值为
的值为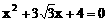 两根,且α,β
两根,且α,β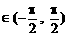 ,则α+β等于
,则α+β等于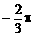 B、
B、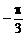 或
或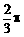 D、
D、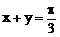 ,则sinx·siny的最小值为
,则sinx·siny的最小值为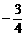 D、
D、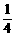
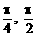 ) B、(
) B、(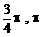 ) C、(
) C、(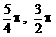 ) D、(
) D、(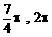 )
)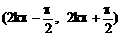 ,k∈Z
,k∈Z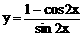 的最小正周期是2π
的最小正周期是2π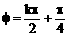 ,k∈Z
,k∈Z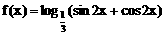 的单调减区间是
的单调减区间是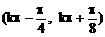 B、
B、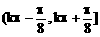 C.
C.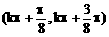 D、
D、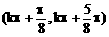 k∈Z
k∈Z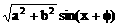 (取
(取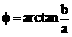 )是常用变形手段。特别是与特殊角有关的sin±cosx,±sinx±
)是常用变形手段。特别是与特殊角有关的sin±cosx,±sinx±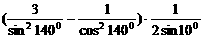 。
。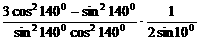
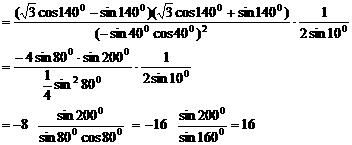
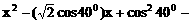
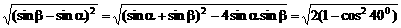
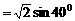
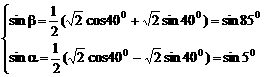
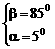
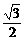
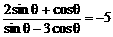 ,求
,求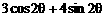 的值。
的值。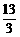
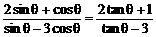
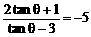
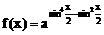 (a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。
(a∈(0,1)),求f(x)的最值,并讨论周期性,奇偶性,单调性。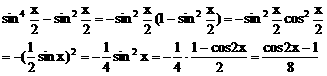
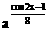
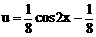
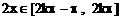 得
得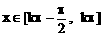 ,此为f(x)的减区间
,此为f(x)的减区间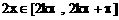 得
得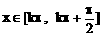 ,此为f(x)增区间
,此为f(x)增区间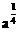
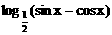
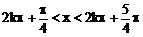 ,k∈Z
,k∈Z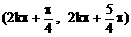 ,k∈Z
,k∈Z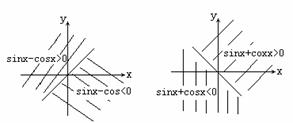 ∵
∵ 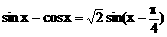
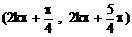 时,
时,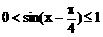
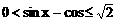
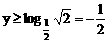
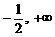 )
)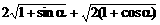 ,α∈(π,2π)
,α∈(π,2π)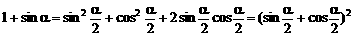
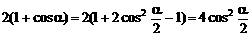
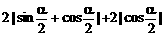
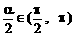
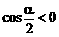
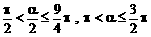 时,
时,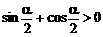
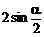
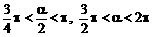 时,
时,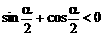
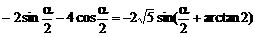
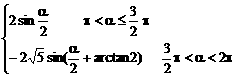
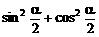 ,是欲擒故纵原则。一般地有
,是欲擒故纵原则。一般地有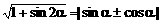 ,
,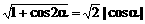 ,
,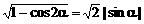 。
。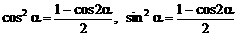 ,可以作为降幂公式使用。
,可以作为降幂公式使用。