0 50942 50950 50956 50960 50966 50968 50972 50978 50980 50986 50992 50996 50998 51002 51008 51010 51016 51020 51022 51026 51028 51032 51034 51036 51037 51038 51040 51041 51042 51044 51046 51050 51052 51056 51058 51062 51068 51070 51076 51080 51082 51086 51092 51098 51100 51106 51110 51112 51118 51122 51128 51136 447348
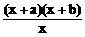 的最小值是______。
的最小值是______。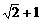 的直角三角形面积的最大值为__________。
的直角三角形面积的最大值为__________。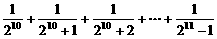 ,则S与1的大小关系是__________。
,则S与1的大小关系是__________。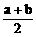 ≥
≥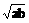 ”的
”的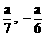 ) B、(
) B、(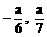 ) C、(
) C、(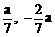 ) D、φ
) D、φ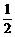 ,b,2ab,a2+b2中最大的是
,b,2ab,a2+b2中最大的是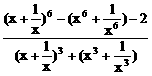 ,则
,则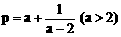 ,
,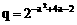 (a>2),则
(a>2),则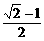 B、
B、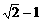 C、
C、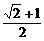 D、
D、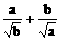 ≥
≥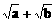 。
。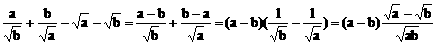
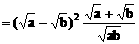 ≥0
≥0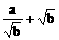 ≥
≥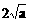
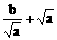 ≥
≥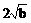
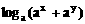 ≤
≤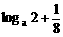 。
。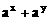 ≥
≥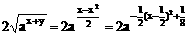 ,
,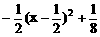 ≤
≤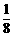 ,0<a<1
,0<a<1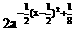 ≥
≥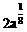
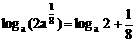
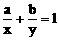 ,求x+y的最小值。
,求x+y的最小值。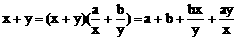 ≥
≥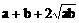 当且仅当
当且仅当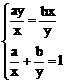 ,即
,即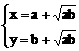 时等号成立
时等号成立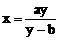
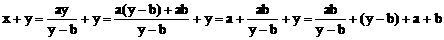
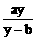 >0得y-b>0
>0得y-b>0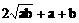
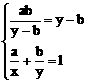 ,即
,即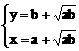 时,等号成立
时,等号成立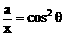 ,
,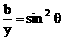 ,
,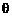 ∈(0,
∈(0,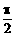 )
)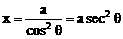 ,
,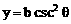
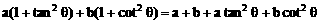 ≥
≥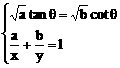 时,等号成立
时,等号成立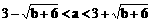
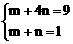
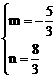
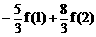
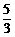 ≤
≤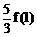 ≤
≤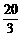 ,
,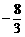 ≤
≤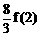 ≤
≤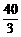
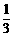 [f(2)-f(1)],c=
[f(2)-f(1)],c=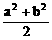 ;
; 或ab≤
或ab≤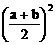 .
. b<a;
b<a; a+c>b+c,此法则又称为移项法则;
a+c>b+c,此法则又称为移项法则;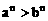 ;
;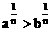 ;
;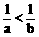 。
。