摘要:三角函数式asinx+bcosx是基本三角函数式之一.引进辅助角.将它化为(取)是常用变形手段.特别是与特殊角有关的sin±cosx.±sinx±cosx.要熟练掌握变形结论. 例3. 求. 解题思路分析: 原式= 注:在化简三角函数式过程中.除利用三角变换公式.还需用到代数变形公式.如本题平方差公式. 例4.已知00<α<β<900.且sinα.sinβ是方程=0的两个实数根.求sin的值. 解题思路分析: 由韦达定理得sinα+sinβ=cos400.sinαsinβ=cos2400- ∴ sinβ-sinα= 又sinα+sinβ=cos400 ∴ ∵ 00<α<β< 900 ∴ ∴ sin=sin600= 注:利用韦达定理变形寻找与sinα.sinβ相关的方程组.在求出sinα.sinβ后再利用单调性求α.β的值. 例5.+5cosβ=0.求tan·tanα的值, (2)已知.求的值. 解题思路分析: (1)从变换角的差异着手. ∵ 2α+β=-α ∴ 8cos[+α]+5cos[-α]=0 展开得: 13coscosα-3sinsinα=0 同除以coscosα得:tantanα= (2)以三角函数结构特点出发 ∵ ∴ ∴ tanθ=2 ∴ 注,齐次式是三角函数式中的基本式.其处理方法是化切或降幂. 例6.已知函数的最值.并讨论周期性.奇偶性.单调性. 解题思路分析: 对三角函数式降幂 ∴ f(x)= 令 则 y=au ∴ 0<a<1 ∴ y=au是减函数 ∴ 由得.此为f(x)的减区间 由得.此为f(x)增区间 ∵ u ∴ f ∴ f(x)为偶函数 ∵ u ∴ f ∴ f(x)为周期函数.最小正周期为π 当x=kπ时.ymin=1 当x=kπ+时.ynax= 注:研究三角函数性质.一般降幂化为y=Asin等一名一次一项的形式.
网址:http://m.1010jiajiao.com/timu3_id_510325[举报]
(2012•洛阳模拟)在△ABC中,角A、B、C所对的边分别为a、b、c,
=(2a,1),
=(2b-c,cosC)且
∥
.
求:
(I)求sinA的值;
(II)求三角函数式
+1的取值范围.
查看习题详情和答案>>
| q |
| p |
| p |
| q |
求:
(I)求sinA的值;
(II)求三角函数式
| -2cos2C |
| 1+tanC |
 (2009•普宁市模拟)三角函数式:①
(2009•普宁市模拟)三角函数式:①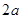 ,1),p=(
,1),p=(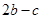 ,
,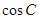 )且
)且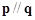 .
.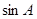 的值;
的值;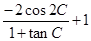 的取值范围?
的取值范围? 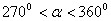 ,三角函数式
,三角函数式 的化简结果为( )
的化简结果为( )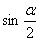 B.
B.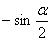 C.
C.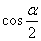 D.
D.