(17)(本小题满分10分)
(Ⅰ)求B的大小;
(Ⅱ)求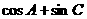 的取值范围.
的取值范围.
(18) (本小题满分12分)
某商场经销某商品,根据以往资料统计,顾客采用的付款期为ζ的分布列为
|
ζ |
1 |
2 |
3 |
4 |
5 |
|
P |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,基利润为200元;分2期或3期付款,基利润为250元;分4期或5期付款,其利润为300元.η表示经销一件该商品的利润.
(Ⅰ)求事件A:“购买该商品的3位顾客中,至少有1件位采用1期付款的概率P(A);
(Ⅱ)求η的分布列及期Eη.
(19)(本小题满分12分)
 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2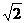 ,SA=SB=
,SA=SB=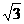 .
.
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.
(20)(本小题满分12分)
设函数f(x)=ex-e- x.
(Ⅰ)证明:f(x)的导数f'(x)≥2;
(Ⅱ)若对所有x=0都有f(x)≥ax,求a的取值范围.
(21本小题满分12分)
已知椭圆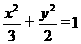 的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
(Ⅰ)设P点的坐标为(x0,y0),证明: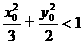 ;
;
(Ⅱ)求四过形ABCD的面积的最小值.
(22)(本小题满分12分)
已知数列{an}中a1=2,an+1=(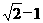 )(an+2),n=1,2,3….
)(an+2),n=1,2,3….
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中b1=2,bn+1=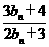 ,n=1,2,3,…,证明:
,n=1,2,3,…,证明:
 ….
….
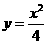 的一条切线的斜率为,则切点的横坐标为
的一条切线的斜率为,则切点的横坐标为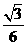 (B)
(B)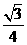 (C)
(C)  (D)
(D) 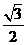
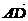 =2
=2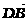 ,
, =
=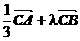 ,则l=
,则l=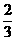 (B)
(B)
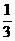 (C) -
(C) -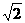 (D)
ln2
(D)
ln2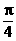 ,
,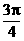 ) (C)
(p,
) (C)
(p,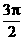 ) (D) (
) (D) (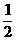 (B) -
(B) - (D)
-
(D)
-