15,(1)解: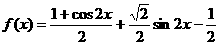 (2分)
(2分)
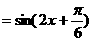 (5分)
(5分)
故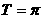 , (6分)
, (6分) 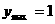 (7分)
(7分)
(2)解: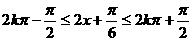 (10分)
(10分)
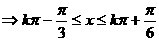 (12分)
(12分)
故增区间为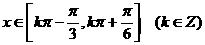 (14分)
(14分)
16,(1)解:设“所选3人中女生人数为0”为事件“ ”,则 (1分)
”,则 (1分)
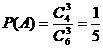 (3分)
(3分)
答:所选人数中女生人数为0时的概率为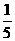 (4分)
(4分)
(2)解: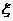 的分布列为
的分布列为
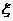 |
0 |
1 |
2 |
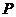 |
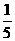 |
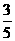 |
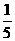 |
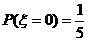 (1分)
(1分)
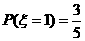 (2分)
(2分)
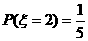 (3分) 列出表格(6分)
(3分) 列出表格(6分)
(3)解:设“所选3人中女生人数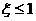 ”为事件“
”为事件“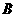 ”(1分)则
”(1分)则
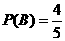 (3分)
(3分)
答:所选3人中女生人数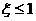 的概率为
的概率为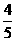 (4)
(4)
本答题卷共4页之第1页
 17(1)解:如图所示建立直角坐标系
17(1)解:如图所示建立直角坐标系
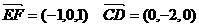
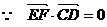 (2分)
(2分)
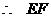 ⊥
⊥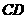 (4分)
(4分)
(2)解:设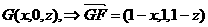 (1分)
(1分)
又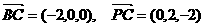
故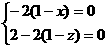
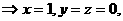 故
故 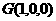 (4分)
(4分)
所以点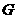 为线段
为线段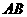 的中点
(5分)
的中点
(5分)
(3)设平面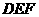 的一个法向量为
的一个法向量为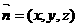 ,
,
又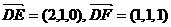
故而有
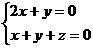 (2分)
(2分)
设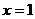 ,则
,则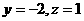
所以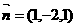 (3分)
(3分)
又因为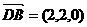 ,设
,设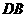 与平面
与平面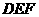 所成的角为
所成的角为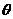
则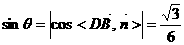 (4分)
(4分)
故所求线面角为 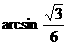 (5分)
(5分)
本答题卷共4页之第2页
18,(1)解:当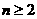 时,
时,
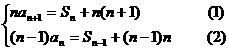 (2分)
(2分)
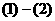
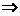
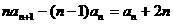
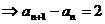 (3分)
(3分)
当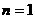 时,
时,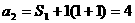 所以
所以 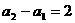
故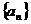 为等差数列 ,得出
为等差数列 ,得出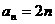 (5分)
(5分)
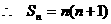 (7分)
(7分)
(2)解:
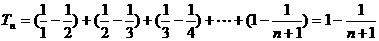 (5分)
(5分)
所以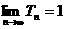 (7分)
(7分)
19 (1)解:由题意得
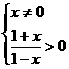 (2分)
(2分)
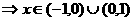 (4分)
(4分)
(2)解:(1)判断:函数在定义域上为奇函数 (1分)
(2)证明:
由上述可知函数的定义域为 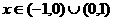 (2分)
(2分)
因为 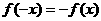
所以函数在定义域上为奇函数 (5分)
(3)解:(1)判断:函数在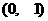 上为减函数
(1分)
上为减函数
(1分)
(2) 证明
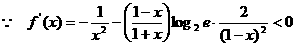
 函数
函数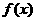 在
在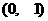 上为减函数
(5分)
上为减函数
(5分)
本答题卷共4页之第3页
20 (1)
解: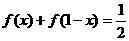 (4分)
(4分)
(2)
解: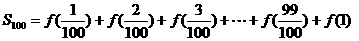 (1)
(1)
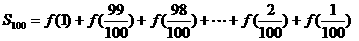 (2)
(2)
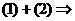
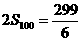 (4分)
(4分)
故而 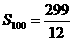 (5分)
(5分)
(3)解:
由(2)式的方法,得出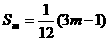 (1分)
(1分)
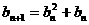
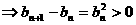 ,
,
所以数列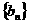 为递增的正数数列
为递增的正数数列
故而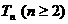 的最小值为
的最小值为 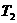 (2分)
(2分)
又因为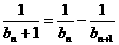 ,所以
,所以 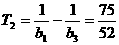 (3分)
(3分)
所以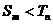 恒成立即只要
恒成立即只要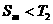 即可
即可
从而有 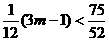
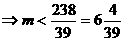 (4分)
(4分)
所以 的最大值为
的最大值为 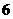 (5分)
(5分)
一,选择题答案为
本试卷共4页之第4页
8.有一道数学难题,学生A解出的概率为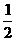 ,学生B解出的概率为
,学生B解出的概率为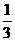 ,学生C解出的概率为
,学生C解出的概率为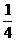 ,若A
,若A  B
B  C三学生独立去解答此题,则恰有1人解出的概率为 ( )
C三学生独立去解答此题,则恰有1人解出的概率为 ( )
A.1 B.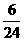 C.
C.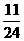 D.
D.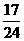
9  5人站成一排,甲
5人站成一排,甲
 乙两人之间恰有1人的不同站法的种数
( )
乙两人之间恰有1人的不同站法的种数
( )
A. 18 B.24 C. 36 D. 48
10  设函数f(x)在定义域内可导,y= f(x)的图象如右图所示,
设函数f(x)在定义域内可导,y= f(x)的图象如右图所示,
则导函数y= f′(x)的图象可能为 ( )
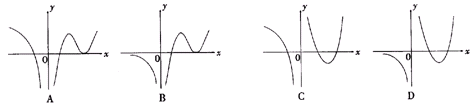
二  填空题:本大题共4小题,每小题4分,共16分
填空题:本大题共4小题,每小题4分,共16分
 把答案填在答题卡的相应位置
把答案填在答题卡的相应位置

11  某工厂生产A
某工厂生产A  B
B  C三种不同型号的产品,产品数量之比依次为2:3:5
C三种不同型号的产品,产品数量之比依次为2:3:5  现用分层抽样方法抽出一个容量为
现用分层抽样方法抽出一个容量为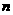 的样本,样本中A种型号产品有16件
的样本,样本中A种型号产品有16件  那么此样本的容量
那么此样本的容量
12 
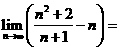 _________
_________ 
|
 一离散型随机变量ξ的概率分布为:
且Eξ=1
一离散型随机变量ξ的概率分布为:
且Eξ=1  5,
5,
则a-b=

14  设函数
设函数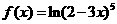 ,则
,则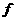 ′
′ =____________________
=____________________
三  解答题:本大题共6小题,每小题14分,共84分
解答题:本大题共6小题,每小题14分,共84分
 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤

15  从4名男生和2名女生中任选3人参加演讲比赛
从4名男生和2名女生中任选3人参加演讲比赛
 设随机变量
设随机变量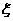 表示所选3人中女生的人数
表示所选3人中女生的人数 
(I)
求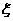 的分布列;
的分布列;
(II)
求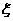 的数学期望;
的数学期望;
(III)
求“所选3人中女生人数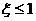 ”的概率
”的概率 
16  已知函数
已知函数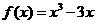

(I)求函数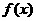 的单调区间;
的单调区间;
(II)求函数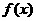 在区间[–3,2]上的最值
在区间[–3,2]上的最值 
17  已知直线
已知直线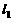 为曲线
为曲线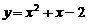 在点
在点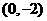 处的切线,
处的切线,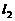 为该曲线的另一条切线,
为该曲线的另一条切线,
且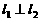

(Ⅰ)求直线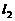 的方程;
的方程;
(Ⅱ)求由直线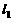

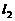 和
和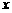 轴所围成的三角形的面积
轴所围成的三角形的面积 
 18
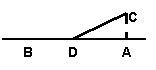
18  :如图,铁路线上AB段长100km,工厂C到铁路的距离CA=20km
:如图,铁路线上AB段长100km,工厂C到铁路的距离CA=20km  现在要
在AB段上某一处D,向C修一条公路,已知铁路与公路原料每吨每千米的运费分别为3元和5元
现在要
在AB段上某一处D,向C修一条公路,已知铁路与公路原料每吨每千米的运费分别为3元和5元
 为了使原料从供应站B运到工厂C的运费最省,D应修在何处?
为了使原料从供应站B运到工厂C的运费最省,D应修在何处?
19  设函数f(x)=x(x-1)(x-a),(a>1)
设函数f(x)=x(x-1)(x-a),(a>1)
(Ⅰ)求导数f¢ (x); 并证明f(x)有两个不同的极值点x1,x2;
(Ⅱ)若不等式f(x1)+ f(x2)£0成立,求a的取值范围 
20  已知数列
已知数列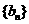 是等差数列
是等差数列
①求数列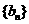 的通项
的通项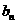 ;
②设数列
;
②设数列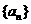 的通项
的通项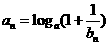 ,记Sn是数列
,记Sn是数列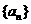 的前n项和
的前n项和 
证明: 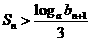 (其中a>1)
(其中a>1)
 14、
14、 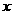
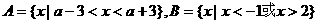 ,若A∪B=R,则实数a的取值范围是 ( )
,若A∪B=R,则实数a的取值范围是 ( )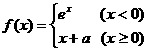 是连续函数,则
是连续函数,则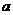 等于( )
等于( )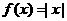 ,在
,在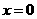 处:
( )
处:
( )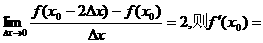 ( )
( )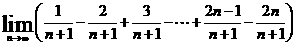 的值为 ( )
的值为 ( )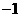 B.
B. C.
C.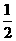 D.
D.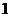
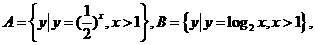 则AÇB等于
则AÇB等于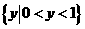 C .
C .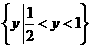 D.
D. 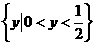
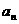 }为等差数列,公差d≠0,{
}为等差数列,公差d≠0,{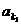 ,
,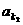 ,
,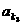 ,……,
,……,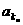 ,……恰为等比数列,其中
,……恰为等比数列,其中 =1,
=1, 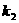 =5,
=5,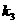 =17,
=17,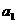 与d的关系
与d的关系 (2)求
(2)求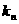 =f (n)的解析式;
=f (n)的解析式; 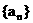 的各项都是正数, 且对任意
的各项都是正数, 且对任意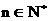 都有
都有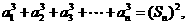 记
记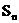 为数列
为数列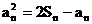
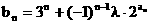 (
(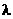 为非零常数,
为非零常数, 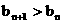

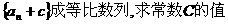
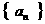 的通项公式
的通项公式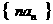 的前n项和
的前n项和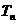
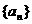 满足
满足
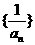 为等差数列;
为等差数列;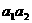 是否是数列
是否是数列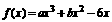 在
在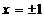 处取得极值;
处取得极值;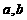 的值;
的值;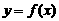 的切线,求此切线方程
的切线,求此切线方程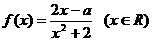 在区间[-1,1]上是增函数
在区间[-1,1]上是增函数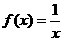 的两根为x1、x2,试问:是否存在实数m,使不等式
的两根为x1、x2,试问:是否存在实数m,使不等式 +tm+1
+tm+1