摘要:(1)解: 故. (2)解: 故增区间为 16.(1)解:设“所选3人中女生人数为0 为事件“ .则 答:所选人数中女生人数为0时的概率为 (2)解:的分布列为 0 1 2 (3)解:设“所选3人中女生人数 为事件“ 则 答:所选3人中女生人数的概率为 (4) 本答题卷共4页之第1页 17(1)解:如图所示建立直角坐标系 ⊥ (2)解:设 又 故 故 所以点为线段的中点 (3)设平面的一个法向量为. 又 故而有 设.则 所以 又因为.设与平面所成的角为 则 故所求线面角为 本答题卷共4页之第2页 18.(1)解:当时. 当时. 所以 故为等差数列 .得出 (2)解: 所以 19 (1)解:由题意得 判断:函数在定义域上为奇函数 (2)证明: 由上述可知函数的定义域为 因为 所以函数在定义域上为奇函数 判断:函数在上为减函数 (2) 证明 函数在上为减函数 本答题卷共4页之第3页 20 (1) 解: (2) 解: (1) (2) 故而 (3)解: 由(2)式的方法.得出 . 所以数列为递增的正数数列 故而的最小值为 又因为 .所以 所以恒成立即只要即可 从而有 所以的最大值为 一.选择题答案为 本试卷共4页之第4页
网址:http://m.1010jiajiao.com/timu3_id_507990[举报]
 ,且对任意实数x,总有
,且对任意实数x,总有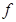 /(x)<3
/(x)<3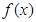 <3x-15的解集为( )
<3x-15的解集为( ) ,且对任意实数x,总有
,且对任意实数x,总有 /(x)<3
/(x)<3 <3x-15的解集为( )
<3x-15的解集为( )