0 50678 50686 50692 50696 50702 50704 50708 50714 50716 50722 50728 50732 50734 50738 50744 50746 50752 50756 50758 50762 50764 50768 50770 50772 50773 50774 50776 50777 50778 50780 50782 50786 50788 50792 50794 50798 50804 50806 50812 50816 50818 50822 50828 50834 50836 50842 50846 50848 50854 50858 50864 50872 447348
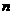 项和
项和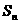 ,则其通项为
,则其通项为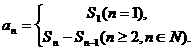 若
若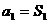 满足
满足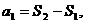 则通项公式可写成
则通项公式可写成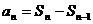 .(2)数列计算是本章的中心内容,利用等差数列和等比数列的通项公式、前
.(2)数列计算是本章的中心内容,利用等差数列和等比数列的通项公式、前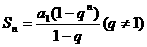 及
及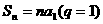 ;已知
;已知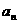 时,也要进行分类;
时,也要进行分类;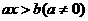 :⑴若
:⑴若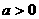 ,则
;⑵若
,则
;⑵若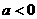 ,则
;
,则
;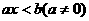 :⑴若
:⑴若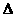 进行讨论:
进行讨论: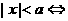 ;
;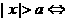 ;
;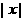 :
;
:
;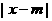 :
;
:
;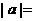 ;②若
;②若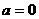 则
则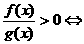 ;⑵
;⑵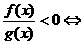 ;
;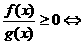 ;⑷
;⑷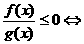 ;
;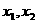 (或更多)但含参数,要分
(或更多)但含参数,要分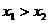 、
、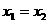 、
、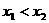 讨论。
讨论。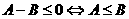
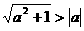 ;
;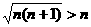
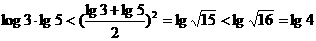 ;
;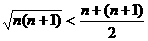
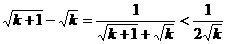 ;
;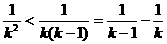 ;
; 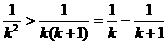 (程度大)
(程度大)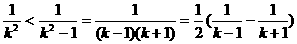 ; (程度小)
; (程度小)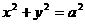 ,可设
,可设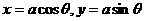 ;
;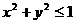 ,可设
,可设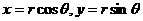 (
(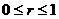 );
);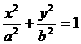 ,可设
,可设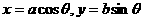 ;
;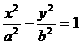 ,可设
,可设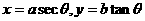 ;
;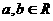 ,则
,则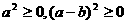 (当且仅当
时取等号)
(当且仅当
时取等号)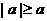 (当且仅当
时取等号);
(当且仅当
时取等号);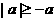 (当且仅当
时取等号)
(当且仅当
时取等号)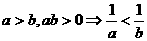 ;
;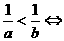 ;
;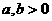 ,则
,则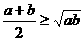 (当且仅当
(当且仅当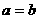 时取等号)
时取等号)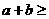 ;
;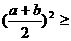 ;
;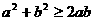 ,
,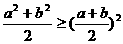
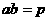 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;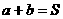 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;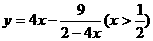 的最小值
。
的最小值
。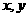 满足
满足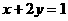 ,则
,则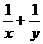 的最小值
。
的最小值
。