21. (山东卷)已知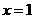 是函数
是函数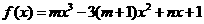 的一个极值点,其中
的一个极值点,其中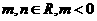 ,
,
(I)求 与
与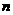 的关系式;
的关系式;
(II)求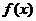 的单调区间;
的单调区间;
(III)当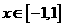 时,函数
时,函数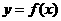 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
解(I)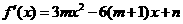 因为
因为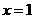 是函数
是函数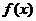 的一个极值点,所以
的一个极值点,所以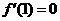 ,即
,即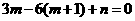 ,所以
,所以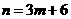
(II)由(I)知,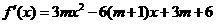 =
=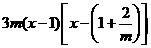
当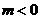 时,有
时,有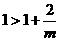 ,当
,当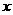 变化时,
变化时,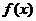 与
与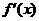 的变化如下表:
的变化如下表:
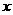 |
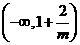 |
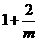 |
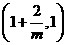 |
1 |
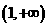 |
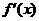 |
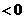 |
0 |
 |
0 |
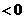 |
|
|
|
|
|
|
|
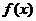 |
调调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
故有上表知,当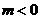 时,
时,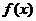 在
在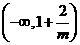 单调递减,在
单调递减,在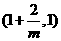 单调递增,在
单调递增,在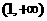 上单调递减.
上单调递减.
(III)由已知得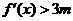 ,即
,即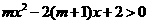
又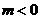 所以
所以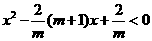 即
即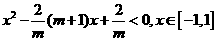 ①
①
设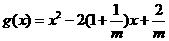 ,其函数开口向上,由题意知①式恒成立,
,其函数开口向上,由题意知①式恒成立,
所以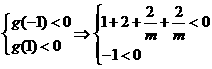 解之得
解之得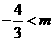 又
又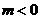 所以
所以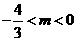
即 的取值范围为
的取值范围为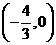
13. ( 全国卷III)已知函数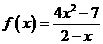 ,
,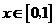
(Ⅰ)求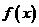 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设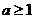 ,函数
,函数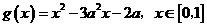 ,若对于任意
,若对于任意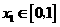 ,总存在
,总存在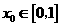 ,使得
,使得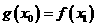 成立,求
成立,求 的取值范围
的取值范围
解:对函数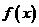 求导,得
求导,得
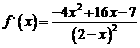
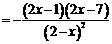
令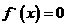 解得
解得 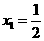 或
或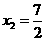
当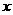 变化时,
变化时,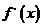 、
、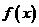 的变化情况如下表:
的变化情况如下表:
|
x |
0 |
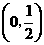 |
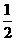 |
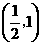 |
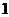 |
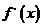 |
|
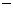 |
0 |
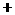 |
|
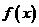 |
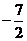 |
 |
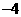 |
 |
 |
所以,当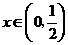 时,
时,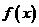 是减函数;当
是减函数;当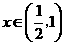 时,
时,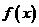 是增函数;
是增函数;
当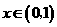 时,
时,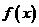 的值域为
的值域为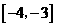
(Ⅱ)对函数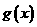 求导,得
求导,得
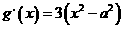
因此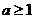 ,当
,当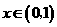 时,
时, 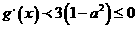
因此当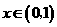 时,
时,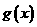 为减函数,从而当
为减函数,从而当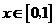 时有
时有
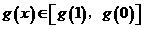
又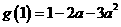 ,
,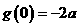 ,即当
,即当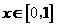 时有
时有
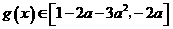
任给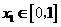 ,
,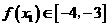 ,存在
,存在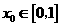 使得
使得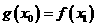 ,则
,则
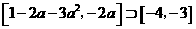
即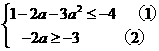
解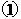 式得
式得 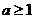 或
或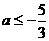
解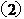 式得
式得 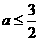
又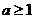 ,
,
故: 的取值范围为
的取值范围为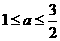
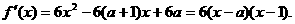
 取得极值, 所以
取得极值, 所以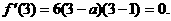 解得
解得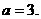
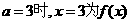 为极值点.
为极值点.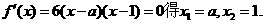
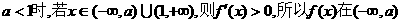 和
和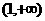 上为增函数,故当
上为增函数,故当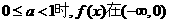 上为增函数.
上为增函数.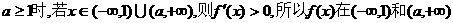 上为增函数,从而
上为增函数,从而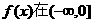 上也为增函数.
上也为增函数. 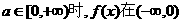 上为增函数.
上为增函数.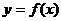 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数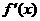 是减函数,且
是减函数,且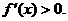 设
设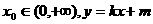 是曲线
是曲线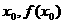 )得的切线方程,并设函数
)得的切线方程,并设函数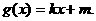
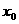 、
、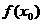 、
、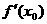 表示m;
表示m;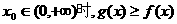 ;
;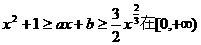 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,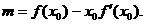 …………………………………………2分
…………………………………………2分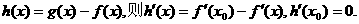
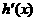 递增,因此,当
递增,因此,当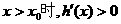 ;
;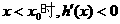 .所以
.所以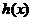 唯一的极值点,且是极小值点,可知
唯一的极值点,且是极小值点,可知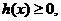 即
即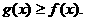 …………………………6分
…………………………6分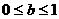 ,
,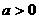 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.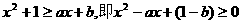 对任意
对任意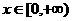 成立的充要条件是
成立的充要条件是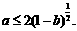
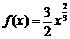 满足前述题设中关于函数
满足前述题设中关于函数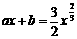 的充要条件是:过点(0,
的充要条件是:过点(0,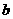 )与曲线
)与曲线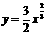 相切的直线的斜率大于
相切的直线的斜率大于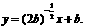
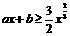 的充要条件是
的充要条件是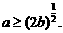 …………………………10分
…………………………10分 对任意
对任意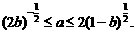 ①
①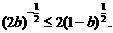 ②
②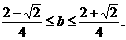 ③
③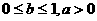 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.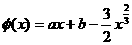 ,于是
,于是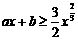 对任意
对任意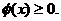 由
由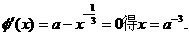
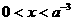 时
时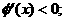 当
当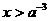 时,
时,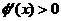 ,所以,当
,所以,当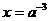 时,
时,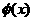 取最小值.因此
取最小值.因此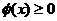 成立的充要条件是
成立的充要条件是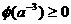 ,即
,即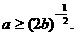 ………………10分
………………10分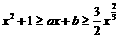 对任意
对任意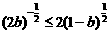 ②
②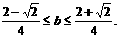
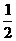 ax2+bx,a≠0.
ax2+bx,a≠0.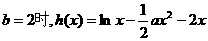 ,
,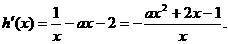
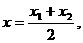
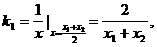
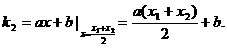
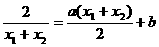 ,则
,则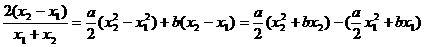
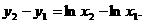
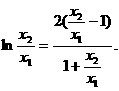 设
设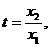 则
则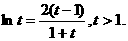 ①
①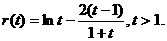 则
则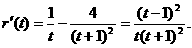
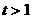 时,
时,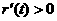 ,所以
,所以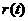 在
在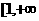 )上单调递增. 故
)上单调递增. 故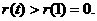
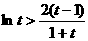 . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.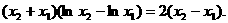
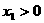 ,所以
,所以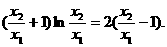
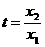 ,得
,得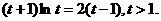 ②
②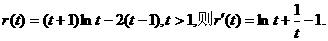
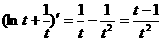 ,所以
,所以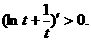
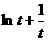 在[1,+
在[1,+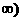 上单调递增.从而
上单调递增.从而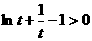 ,即
,即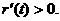
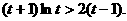 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.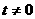 ,点P(
,点P(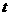 ,0)是函数
,0)是函数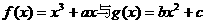 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.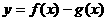 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求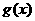 的图象都过点(
的图象都过点(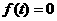 ,
,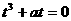 .因为
.因为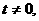 所以
所以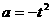 .
.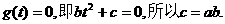
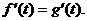
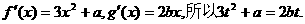
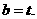 因此
因此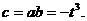 故
故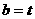 ,
,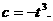
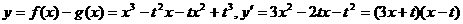 .
.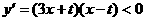 时,函数
时,函数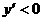 ,若
,若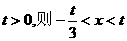 ;若
;若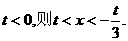
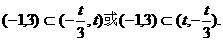
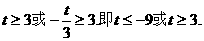
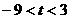 时,函数
时,函数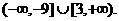
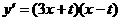 是(-1,3)
是(-1,3)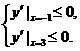 即
即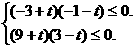 解得
解得
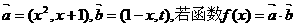 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.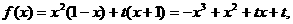
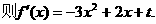
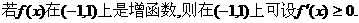
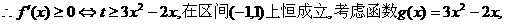
 开口向上的抛物线,故要使
开口向上的抛物线,故要使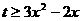 在区间
在区间
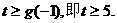
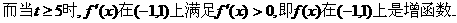
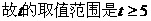 .
.
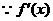 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,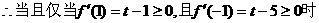
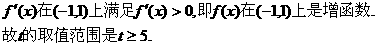
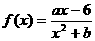 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.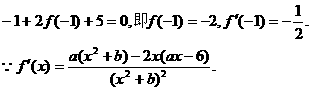

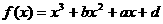 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为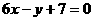 .
.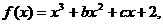
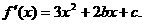
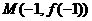 处的切线方程是
处的切线方程是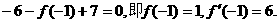
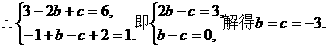
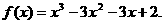
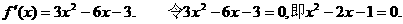
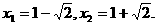 当
当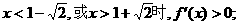
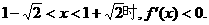
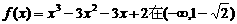 内是增函数,在
内是增函数,在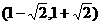 内是减函数,
内是减函数,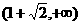 内是增函数.
内是增函数.