摘要:18.设.点P(.0)是函数的图象的一个公共点.两函数的图象在点P处有相同的切线. (Ⅰ)用表示a.b.c, (Ⅱ)若函数在上单调递减.求的取值范围. 解:(I)因为函数.的图象都过点(.0).所以. 即.因为所以. 又因为.在点(.0)处有相同的切线.所以 而 将代入上式得 因此故.. (II)解法一. 当时.函数单调递减. 由.若,若 由题意.函数在上单调递减.则 所以 又当时.函数在上单调递减. 所以的取值范围为 解法二: 因为函数在上单调递减.且是 上的抛物线. 所以 即解得 所以的取值范围为
网址:http://m.1010jiajiao.com/timu3_id_501296[举报]
 ,点P(
,点P( ,0)是函数
,0)是函数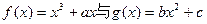 的图象的一个公共点,两函数的图象在点P处有相同的切线.(Ⅰ)用
的图象的一个公共点,两函数的图象在点P处有相同的切线.(Ⅰ)用