0 50091 50099 50105 50109 50115 50117 50121 50127 50129 50135 50141 50145 50147 50151 50157 50159 50165 50169 50171 50175 50177 50181 50183 50185 50186 50187 50189 50190 50191 50193 50195 50199 50201 50205 50207 50211 50217 50219 50225 50229 50231 50235 50241 50247 50249 50255 50259 50261 50267 50271 50277 50285 447348
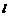 与y轴交于点M. 若
与y轴交于点M. 若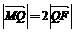 ,求直线
,求直线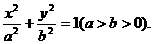
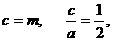 所以
所以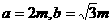 .
.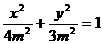
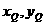 ),直线
),直线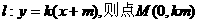
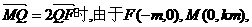 由定比分点坐标公式,得
由定比分点坐标公式,得
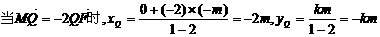 .
.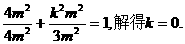 故直线l的斜率是0,
故直线l的斜率是0,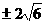 .
.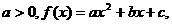 曲线
曲线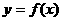 在点
在点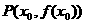 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为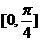 ,则
,则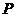 到曲线
到曲线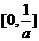 (B
(B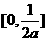 )
(C
)
(C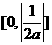 )
(D)
)
(D) 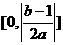
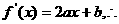 过P点的切线斜率
过P点的切线斜率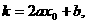 由题意:
由题意: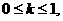
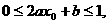
 又
又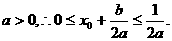 ∵
∵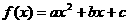 的对称轴为
的对称轴为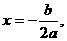
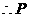 到该对称轴的距离为
到该对称轴的距离为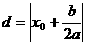
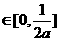 ,故应选B.
,故应选B.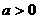 ,向量
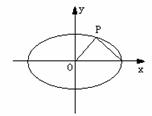
,向量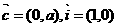 ,经过原点O以
,经过原点O以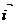
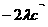 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中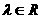 。试问:是否存在两个定点
。试问:是否存在两个定点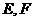 ,使得
,使得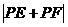 为定值?若存在,求出
为定值?若存在,求出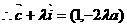 ,
, 直线OA和AP的方程分别为:
直线OA和AP的方程分别为: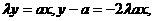 消去参数
消去参数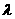 得P点的轨迹方程为:
得P点的轨迹方程为: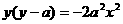 ,整理得
,整理得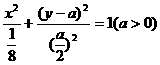 (*)
(*)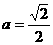 时,方程(*)表示圆,故不存在满足题意的两定点E和F;
时,方程(*)表示圆,故不存在满足题意的两定点E和F;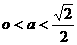 时,方程(*)表示焦点在
时,方程(*)表示焦点在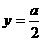 上的椭圆,两焦点
上的椭圆,两焦点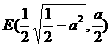 和
和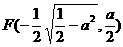 即为满足题意的两定点;
即为满足题意的两定点;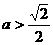 时,方程(*)表示焦点在
时,方程(*)表示焦点在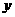 轴上的椭圆,两焦点
轴上的椭圆,两焦点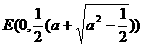 和
和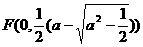 即为满足题意的两定点。
即为满足题意的两定点。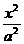 +
+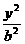 =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线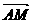 =λ
=λ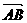 .
.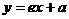 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是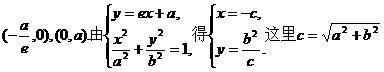 .
.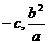 ). 由
). 由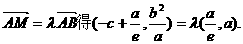

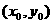 ,
,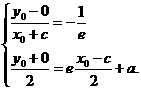 ,
,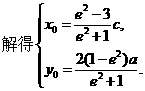
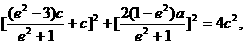
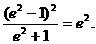
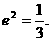
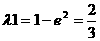

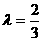 时,△PF1F2为等腰三角形
时,△PF1F2为等腰三角形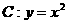 的焦点为F,动点P在直线
的焦点为F,动点P在直线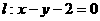 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.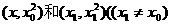 ,
,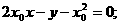
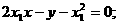
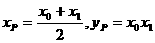
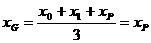 ,
,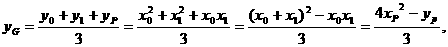
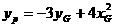 ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为: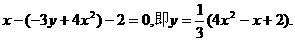
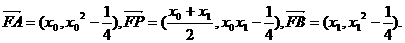
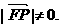
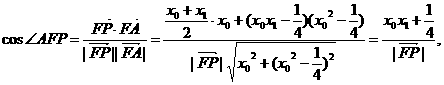
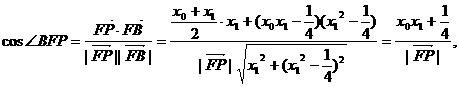
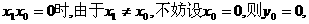 所以P点坐标为
所以P点坐标为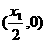 ,则P点到直线AF的距离为:
,则P点到直线AF的距离为:
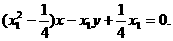
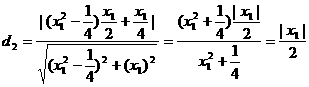
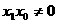 时,直线AF的方程:
时,直线AF的方程:
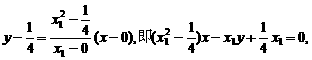
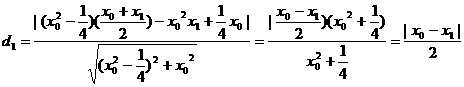 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离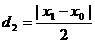 ,因此由d1=d2,可得到∠AFP=∠PFB
,因此由d1=d2,可得到∠AFP=∠PFB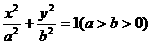 上动点P作⊙
上动点P作⊙ :
: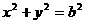 的两条切线
的两条切线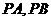 ,切点为
,切点为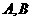 ,若直线
,若直线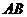 与
与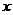 轴、
轴、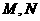 两点;
两点;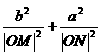 为定值;
为定值;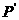 ,使得由
,使得由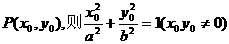 易知
易知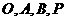 四点共圆,并且此圆的方程为
四点共圆,并且此圆的方程为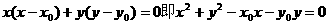 ,由于
,由于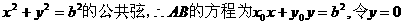 得
得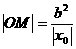 ,令
,令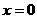 得
得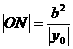 ,故
,故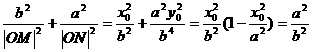 (定值)。
(定值)。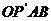 为正方形,
为正方形,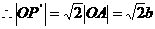 ,从而存在点
,从而存在点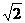 为半径的圆与椭圆相交,
为半径的圆与椭圆相交,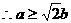 ,故
,故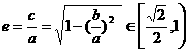 。
。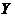 轴上的抛物线
轴上的抛物线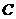 截直线
截直线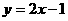 所得的弦长为
所得的弦长为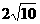 。
。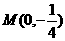 ,且斜率
,且斜率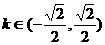 的直线与抛物线C相交与A、B两点,求M分
的直线与抛物线C相交与A、B两点,求M分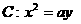 ,直线与抛物线C交于
,直线与抛物线C交于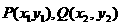 ,由
,由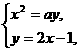
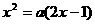 ,即
,即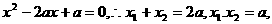
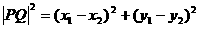
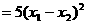 ,
,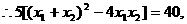 即
即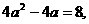 解得
解得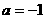 或
或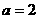 ,
,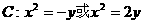 。
。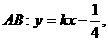 把它代入
把它代入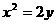 得
得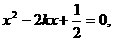 ∵
∵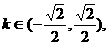
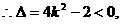 不合。把
不合。把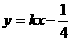 代入
代入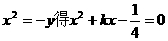 ,设
,设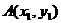 ,
, 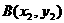 ,则
,则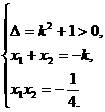 (*) 由定比分点公式:0=
(*) 由定比分点公式:0=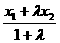 ,
,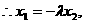 代入(*)的
代入(*)的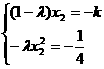 ,显然
,显然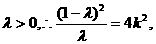 又
又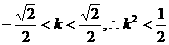 ,于是
,于是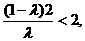 即
即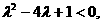 故
故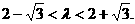
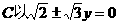 为渐近线且过点
为渐近线且过点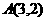 。
。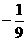 ,求动点
,求动点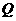 ,使得
,使得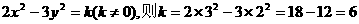 ,故
,故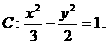
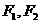 为焦点的椭圆,设方程为:
为焦点的椭圆,设方程为: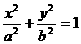 ,则
,则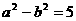 ①
①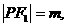
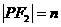 ,则
,则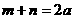 ,
,
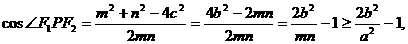 知当
知当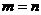 即P为椭圆短轴端点时,
即P为椭圆短轴端点时,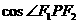 有最小值,并且
有最小值,并且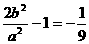 ②,由①,②可得
②,由①,②可得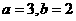 ,故动点P的轨迹方程为:
,故动点P的轨迹方程为: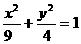 。
。 是以上轨迹上任一点,则
是以上轨迹上任一点,则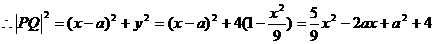 ,又
,又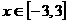 ,
,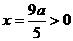 。
。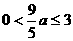 即
即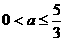 ,则当
,则当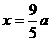 时,
时,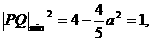
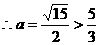 ,不合。
,不合。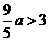 ,即
,即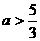 ,则当
,则当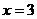 时,
时,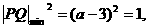
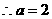 或
或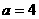 。
。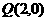 或
或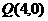 满足条件。
满足条件。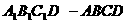 的侧面
的侧面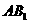 内有
内有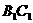 距离相等,则动点
距离相等,则动点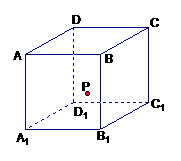
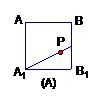
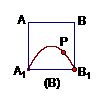
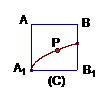
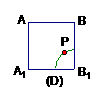
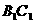 ⊥面
⊥面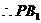 即为点
即为点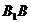 中点的抛物线,又点
中点的抛物线,又点 显然在此抛物线上,故选
显然在此抛物线上,故选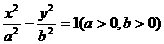 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是( )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是( )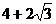 B.
B.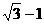 C.
C.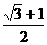 D.
D.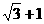
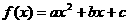 (其中
(其中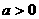 )的图象与
)的图象与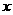 轴有两个不同的公共点,若
轴有两个不同的公共点,若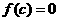 ,且
,且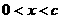 时,
时,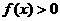 ;
;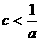 ; (2)求证:
; (2)求证: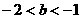
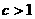 ,
,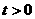 时,有
时,有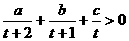
 已知椭圆
已知椭圆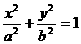
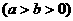 ,与
,与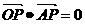 (O为原点),求离心率的取值范围。
(O为原点),求离心率的取值范围。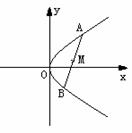 定长为3的线段AB的两个端点在抛物线
定长为3的线段AB的两个端点在抛物线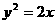 上移动,M为线段AB的中点。求M点到
上移动,M为线段AB的中点。求M点到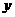 轴的最短距离。
轴的最短距离。