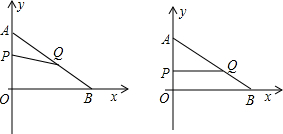摘要：如图.在平面直解坐标系中.四边形OABC为矩形.点A.B的坐标分别为.动点M.N分别从点O.B同时出发.以每秒1个单位的速度运动.其中点M沿OA向终点A运动.点N沿BC向终点C运动.过点N作NPBC.交AC于点P.连结MP.当两动点运动了t秒时. (1)P点的坐标为(4-t,). (2)记△MPA的面积为S.求S与t的函数关系式 (3)当t= 秒时.S有最大值.最大值是 (4)若点Q在y轴上.当S有最大值且△QAN为等腰三角形时.求直线AQ的解析式. (1)4-t, t (2)S=MA·PD=(4-t)t S= (3)当t===2s S有最大值, S最大= ①AN=AQ AN2=AQ2 22+32=16+M2 M2=-3 ∴此方程无解,故此情况舍去. ②AN=NQ AN2=NQ2 13=22+(3-m)2 3-m=± m=0,m2=6 ∴Q=(0,0) ∴AQ:y=0 ③NQ=AQ 4+(3-M)2=16+M2 M=- ∴(0, ) AQ:y=2x
网址：http://m.1010jiajiao.com/timu3_id_488954[举报]
如图，在平面角直角坐标系中，A（-2，0），B（0，3），C（3，0），D（0，2）．
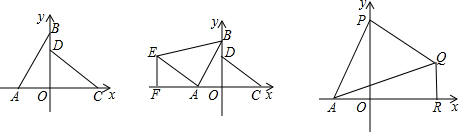
（1）求证：AB=CD且AB⊥CD；
（2）以A为直角顶点在第二象限内作等腰直角三角形ABE，过点E作EF⊥x轴于点F，求点F的坐标；
（3）若点P为y轴正半轴上一动点，以AP为直角边作等腰直角三角形APQ，∠APQ=90°，QR⊥x轴于点R，当点P运动时，OP-QR的值是否发生变化？若不变，求出其值；若变化，请说明理由．
查看习题详情和答案>>
（1）求证：AB=CD且AB⊥CD；
（2）以A为直角顶点在第二象限内作等腰直角三角形ABE，过点E作EF⊥x轴于点F，求点F的坐标；
（3）若点P为y轴正半轴上一动点，以AP为直角边作等腰直角三角形APQ，∠APQ=90°，QR⊥x轴于点R，当点P运动时，OP-QR的值是否发生变化？若不变，求出其值；若变化，请说明理由．
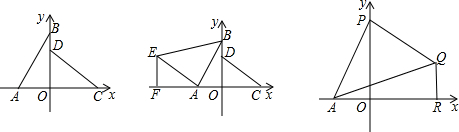
（2013•鞍山一模）如图，在平面直角着坐标系中，一次函数y=| 3 |
| 3 |
（1）求点C的点坐标．
（2）若点P是线段BC延长线上一动点，连接AP，作线段AP的垂直平分线，交AP于点D，交y轴于点E，连接EA，EP，EC，EC交AP于点F．
①点P在移动过程中，∠AEP的角度是否发生变化？为什么？
②若S△AEF-S△CFP=2
| 3 |
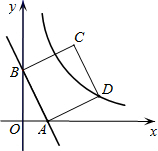方形，曲线y=