摘要:( 2010年山东菏泽全真模拟1) 如图1.在平面直角坐标系中.已知点.点在正半轴上.且.动点在线段上从点向点以每秒个单位的速度运动.设运动时间为秒.在轴上取两点作等边. (1)求直线的解析式, (2)求等边的边长(用的代数式表示).并求出当等边的顶点运动到与原点重合时的值, (3)如果取的中点.以为边在内部作如图2所示的矩形.点在线段上.设等边和矩形重叠部分的面积为.请求出当秒时与的函数关系式.并求出的最大值. 答案:解:(1)直线的解析式为:. (2)方法一.... . . 是等边三角形.. .. 方法二.如图1.过分别作轴于.轴于. 可求得. . . 当点与点重合时. . . . . (3)①当时.见图2. 设交于点. 重叠部分为直角梯形. 作于. .. . . . . . . . 随的增大而增大. 当时.. ②当时.见图3. 设交于点. 交于点.交于点. 重叠部分为五边形. 方法一.作于.. . . . 方法二.由题意可得.... 再计算 . . .当时.有最大值.. ③当时..即与重合. 设交于点.交于点.重叠部 分为等腰梯形.见图4. . 综上所述:当时., 当时., 当时.. . 的最大值是.
网址:http://m.1010jiajiao.com/timu3_id_488951[举报]
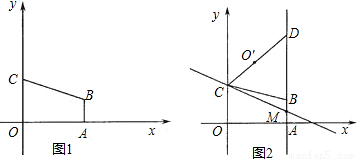
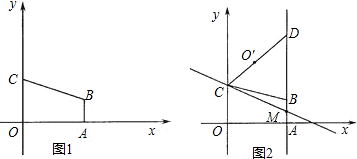
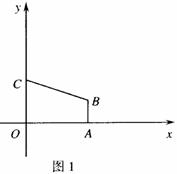
如图1,在平面直角坐标中,直角梯形OABC的顶点A的坐标为(4,0),直线y=-
x+3经过顶点B,与y轴交于顶点C,AB∥OC.
(1)求顶点B的坐标;
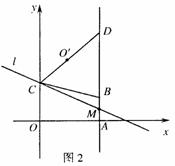
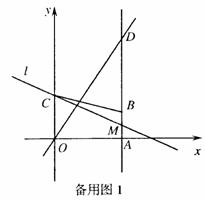
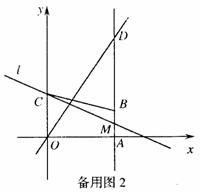
(2)如图2,直线l经过点C,与直线AB交于点M,点O?为点O关于直线l的对称点,连接CO?,并延长交直线AB于第一象限的点D,当CD=5时,求直线l的解析式;
(3)在(2)的条件下,点P在直线l上运动,点Q在直线OD上运动,以P、Q、B、C为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
| 1 | 4 |
(1)求顶点B的坐标;
(2)如图2,直线l经过点C,与直线AB交于点M,点O?为点O关于直线l的对称点,连接CO?,并延长交直线AB于第一象限的点D,当CD=5时,求直线l的解析式;
(3)在(2)的条件下,点P在直线l上运动,点Q在直线OD上运动,以P、Q、B、C为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
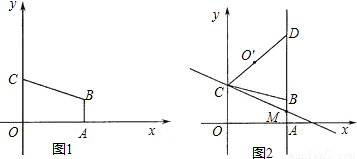
如图1,在平面直角坐标中,直角梯形OABC的顶点A的坐标为(4,0),直线y=- x+3经过顶点B,与y轴交于顶点C,AB∥OC.
x+3经过顶点B,与y轴交于顶点C,AB∥OC.
(1)求顶点B的坐标;
(2)如图2,直线l经过点C,与直线AB交于点M,点O´为点O关于直线l的对称点,连接CO´,并延长交直线AB于第一象限的点D,当CD=5时,求直线l的解析式;
(3)在(2)的条件下,点P在直线l上运动,点Q在直线OD上运动,以P、Q、B、C为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,说明理由.
查看习题详情和答案>>
 x+3经过顶点B,与y轴交于顶点C,AB∥OC.
x+3经过顶点B,与y轴交于顶点C,AB∥OC.(1)求顶点B的坐标;
(2)如图2,直线l经过点C,与直线AB交于点M,点O´为点O关于直线l的对称点,连接CO´,并延长交直线AB于第一象限的点D,当CD=5时,求直线l的解析式;
(3)在(2)的条件下,点P在直线l上运动,点Q在直线OD上运动,以P、Q、B、C为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,说明理由.

查看习题详情和答案>>
 x+3经过顶点B,与y轴交于顶点C,AB∥OC.
x+3经过顶点B,与y轴交于顶点C,AB∥OC.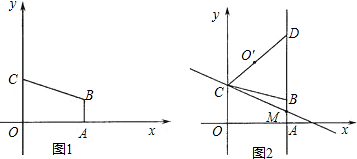
 x+3经过顶点B,与y轴交于顶点C,AB∥OC.
x+3经过顶点B,与y轴交于顶点C,AB∥OC.