0 48785 48793 48799 48803 48809 48811 48815 48821 48823 48829 48835 48839 48841 48845 48851 48853 48859 48863 48865 48869 48871 48875 48877 48879 48880 48881 48883 48884 48885 48887 48889 48893 48895 48899 48901 48905 48911 48913 48919 48923 48925 48929 48935 48941 48943 48949 48953 48955 48961 48965 48971 48979 447348
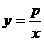 (p>0)的图象与直线AB交于C、D两点,连结
(p>0)的图象与直线AB交于C、D两点,连结 这个最大值;
这个最大值; 所以S=
所以S=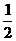 mn,
mn,
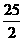
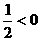 , ∴ 当n=5时,S取最大值
, ∴ 当n=5时,S取最大值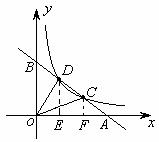 (2)设直线AB的解析式为
(2)设直线AB的解析式为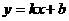 ,
,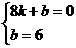 ,
,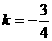 ,
,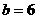 ,
,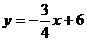 .
. 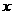 轴的垂线,垂足分别点E、F,
轴的垂线,垂足分别点E、F,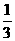 S△AOB ,即
S△AOB ,即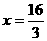 .
.
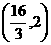
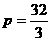
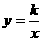 和一次函数
和一次函数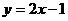 ,其中一次函数的图像经过点(k,5).
,其中一次函数的图像经过点(k,5).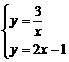 解这个方程组得:
解这个方程组得: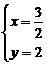 或
或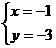
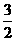 ,2)
,2)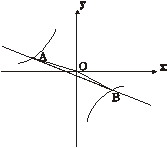 (2010福建模拟)如图,一次函数
(2010福建模拟)如图,一次函数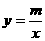 的图象交于A(-3,1)、B(2,n)两点.
的图象交于A(-3,1)、B(2,n)两点.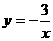
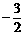 又∵B(2, n) ∴ n=
又∵B(2, n) ∴ n=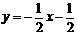 ∴
∴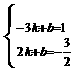 解之得:
解之得: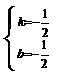
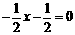 (2)由(1)知
, ∴当y=0时, ∴
(2)由(1)知
, ∴当y=0时, ∴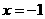
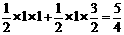
 (2010年吉林中考模拟题)如图,在直角坐标系中,△OBA∽△DOC,
(2010年吉林中考模拟题)如图,在直角坐标系中,△OBA∽△DOC,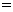
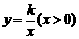 的图象经过点D,
的图象经过点D, E的长.
E的长.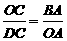 .
.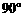 ,∴
,∴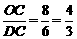 .
.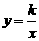 的图象上,∴
的图象上,∴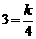
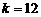 .
.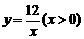 图象与AB的交点,∴AE
图象与AB的交点,∴AE
 ∴BE
∴BE 与函数
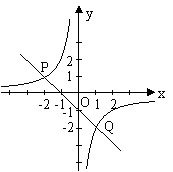
与函数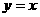 和函数
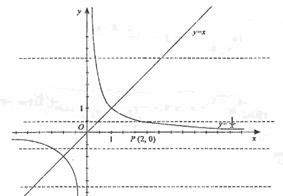
和函数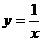 的图象分别交于点A和点B,又有定点P(2,0) .
的图象分别交于点A和点B,又有定点P(2,0) .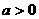 ,且tan∠POB=
,且tan∠POB=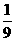 ,求线段AB的长;
,求线段AB的长;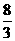 ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;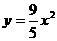 的图象,求点P到直线AB的距离 .
的图象,求点P到直线AB的距离 . 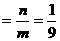 ,得m=9n,又点B在函数
,得m=9n,又点B在函数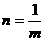 ,所以m=3(-3舍去),点B为
,所以m=3(-3舍去),点B为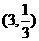 ,
,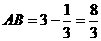 ;
;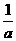 ,a),则AB=
,a),则AB=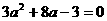 ,解得
,解得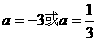 .
. ,点A(―3,―3),B(―
,点A(―3,―3),B(―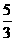 ,-
,-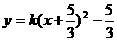 ,点A代入,解得k= -
,点A代入,解得k= -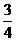 ,所以所求函数解析式为
,所以所求函数解析式为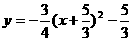 .
. 同理,当a =
同理,当a = 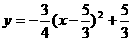 ;
;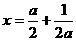 .
.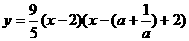 .
.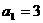 ,
,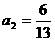 ,所以点P到直线AB的距离为3或
,所以点P到直线AB的距离为3或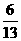
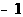 ),且P(
),且P(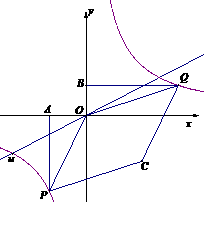 (3)当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.
(3)当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.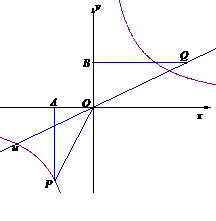
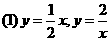 ;
;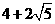 .
.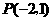 和
和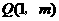 .
.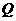 点的坐标;
点的坐标;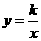 ,
, 反比例函数图象经过点
反比例函数图象经过点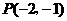 .
.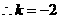 .
. 反比例函数关第式
反比例函数关第式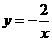 .
.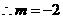 .
.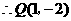 .
.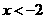 或
或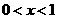 时,一次函数的值大于反比例函数的值.
时,一次函数的值大于反比例函数的值.