16.(2010北京市朝阳区模拟)一辆经营长途运输的货车在高速公路的 处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油量
处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油量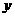 (升)与行驶时间
(升)与行驶时间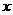 (时)之间的关系:
(时)之间的关系:
行驶时间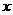 (时) (时) |
0 |
1 |
2 |
2.5 |
余油量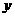 (升) (升) |
100 |
80 |
60 |
50 |
(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示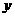 与
与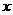 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(2)按照(1)中的变化规律,货车从 处出发行驶4.2小时到达B处,求此时油箱内余油多少升?
处出发行驶4.2小时到达B处,求此时油箱内余油多少升?
解:(1)设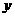 与
与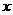 之间的关系为一次函数,其函数表达式为
之间的关系为一次函数,其函数表达式为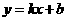
将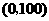 ,
,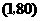 代入上式得,
代入上式得,
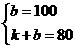 解得
解得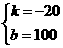
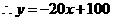
验证:当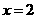 时,
时,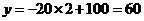 ,符合一次函数
,符合一次函数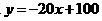 ;
;
当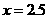 时,
时,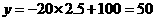 ,也符合一次函数
,也符合一次函数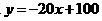 .
.
 可用一次函数
可用一次函数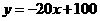 表示其变化规律,而不用反比例函数、二次函数表示其变化规律
表示其变化规律,而不用反比例函数、二次函数表示其变化规律
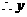 与
与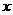 之间的关系是一次函数,其函数表达式为
之间的关系是一次函数,其函数表达式为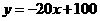
(2)当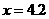 时,由
时,由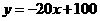 可得
可得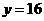
即货车行驶到B处时油箱内余油16升.
12.(2010浙江杭州) 如图1, 在底面积为l00cm2、高为20cm的长方体水槽内放人一个圆柱形烧杯.以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止
在底面积为l00cm2、高为20cm的长方体水槽内放人一个圆柱形烧杯.以恒定不变的流量速度先向烧杯中注水,注满烧杯后,继续注水,直至注满水槽为止 ,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h与注水时间t之间的函数关系如图2所示.
,此过程中,烧杯本身的质量、体积忽略不计,烧杯在大水槽中的位置始终不改变.水槽中水面上升的高度h与注水时间t之间的函数关系如图2所示.
(1)写出函数图象中点A、点B的实际意义;
(2)求烧杯的底面积;
 (3)若烧杯的高为9cm,求注水的速度及注满水槽所用的时间.
(3)若烧杯的高为9cm,求注水的速度及注满水槽所用的时间.
|
解:(1)点A:烧杯中刚好注满水
点B:水槽中水面恰与烧杯中水面齐平
(2)由图可知:烧杯放满需要18 s,水槽水面与烧杯水面齐平,需要90 s
∴ 可知,烧杯底面积:长方体底面积=1:5
∴ 烧杯的底面积为20 cm2
(3)注水速度为10 cm3/s,注满水槽所需时间为200 s
11.(2010年武汉市中考拟)已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产甲、乙两种型号的时装共80套.已知做一套甲种型号的时装或一套乙种型号的时装所需A、B两种布料如下表:
|
布料
时装 |
甲 |
乙 |
|
A种(米) |
0.6 |
1.1 |
|
B种(米) |
0.9 |
0.4 |
若销售一套甲种型号的时装可获利润45元,销售一套乙种型号的时装可获利润50元.设生产乙种型号的时装为x套,用这批布料生产这两种型的时装所为y元.
(1)写出y(元)与x(套)的函数关系式,并写出自变量的取值范围;
(2)雅美服装厂在生产这批时装中,当生产两种型号的时装各多少套时,获得的总利润最大?最大利润是 多少元?
多少元?
答案:(1)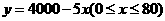 的整数
的整数
(2)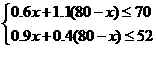 得
得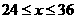 ,当x=24时,利润最大是3880
,当x=24时,利润最大是3880
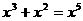 B.
B.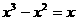 C.
C.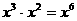 D.
D.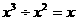
 的
的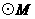 与
与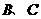 把弧OA分为三等分,连结
把弧OA分为三等分,连结 并延长交
并延长交 ;
; 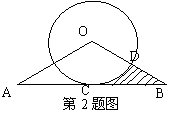 (2)若直线
(2)若直线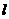 :
: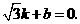
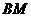 ,∵OA是直径,且
,∵OA是直径,且 ,
,
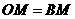 ,∴
,∴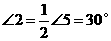 ,
, 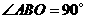 ,∴
,∴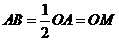 ,
,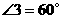 ,
, 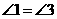 ,
,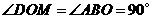 ,
,
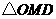 和
和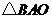 中,
中,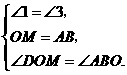
 ∴
∴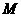 ,
,
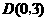 ,
,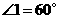 ,
,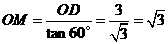 ,
, 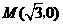 ,
,
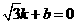 .
. 桃巧克力需可可粉13克,需核桃
桃巧克力需可可粉13克,需核桃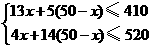
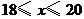
 为整数
为整数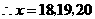 当
当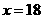 时,
时,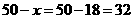
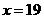 时,
时,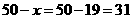
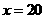 时,
时,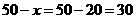
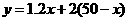
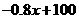
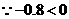
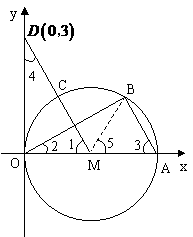
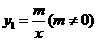 的图象经过点A(-2,1),一次函数
的图象经过点A(-2,1),一次函数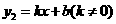 的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.
的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.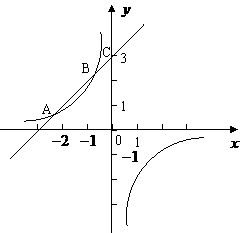
 点A(-2,1)在反比例函数
点A(-2,1)在反比例函数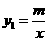 的图象上.
的图象上.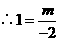 即
即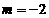
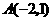 ,
,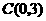 在一次函数
在一次函数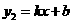 图象上.
图象上.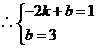 即
即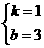
 反比例函数与一次函数解析式分别为:
反比例函数与一次函数解析式分别为: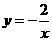 与
与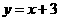
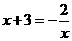 ,即
,即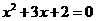
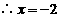 或
或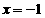 于是
于是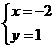 或
或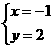
 (2)设公司可安排员工a人,定价
(2)设公司可安排员工a人,定价 )在直线
)在直线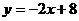 上.
上.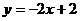 ;(2)
;(2)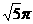 ;
;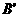 (-1, -5),
(-1, -5), (7,-1),
(7,-1),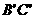 的函数解析式为
的函数解析式为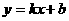 ,
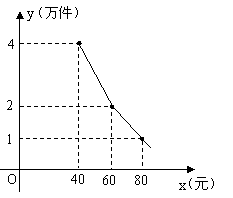
,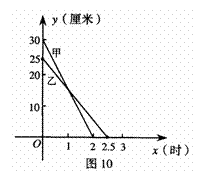 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题: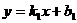 。由图可知,函数的图象过点(2,0),(0,30),∴
。由图可知,函数的图象过点(2,0),(0,30),∴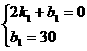 ,解得
,解得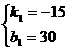 ∴ y=-15x+30
∴ y=-15x+30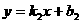 。由图可知,函数的图象过点(2.5,0),(0,25),∴
。由图可知,函数的图象过点(2.5,0),(0,25),∴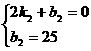 ,解得
,解得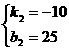 ∴ y=-10x+25
∴ y=-10x+25