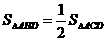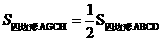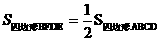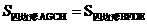0 48728 48736 48742 48746 48752 48754 48758 48764 48766 48772 48778 48782 48784 48788 48794 48796 48802 48806 48808 48812 48814 48818 48820 48822 48823 48824 48826 48827 48828 48830 48832 48836 48838 48842 48844 48848 48854 48856 48862 48866 48868 48872 48878 48884 48886 48892 48896 48898 48904 48908 48914 48922 447348
 如上图,甲船在港口P的北偏西600方向,距港口80海里的A处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P出发,沿北偏东450方向匀速驶离港口P,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(精确到0.1海里/时,参考数据
如上图,甲船在港口P的北偏西600方向,距港口80海里的A处,沿AP方向以12海里/时的速度驶向港口P.乙船从港口P出发,沿北偏东450方向匀速驶离港口P,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(精确到0.1海里/时,参考数据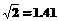 ,
,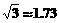 )
)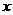 海里/时,2小时后甲船在点
海里/时,2小时后甲船在点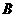 处,乙船在点
处,乙船在点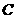 处,作
处,作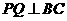 于
于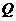 ,则
,则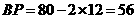 海里,
海里,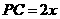 海里.
海里.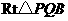 中,
中,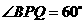 ,
,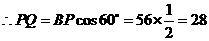 .
. 中,
中, ,
,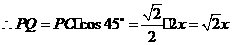 .
.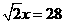 ,
,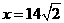 .
.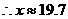 .
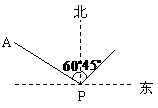
.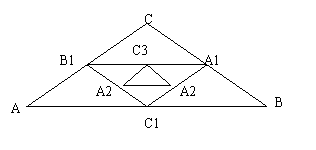 (2010广东省中考拟).如图,在△ABC中,∠C=900,AC=8,BC=6,分别取各边的中点A1,B1,C1,得到△A1B1C1,再取△A1B1C1各边中点A2,B2,C2,得到△A2B2C2,按此作法进行下去,得到△A3B3C3,………,△AnBnCn.
(2010广东省中考拟).如图,在△ABC中,∠C=900,AC=8,BC=6,分别取各边的中点A1,B1,C1,得到△A1B1C1,再取△A1B1C1各边中点A2,B2,C2,得到△A2B2C2,按此作法进行下去,得到△A3B3C3,………,△AnBnCn.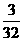 和
和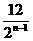
 010年武汉市中考拟)图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合)。
010年武汉市中考拟)图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合)。 旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于F(图2);
旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于F(图2);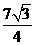 ?
? N·E
N·E
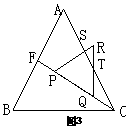 ∴∠QTC=30° ∴∠QTC=∠TCQ ∴QT=QC=x∴ RT=3-x
∴∠QTC=30° ∴∠QTC=∠TCQ ∴QT=QC=x∴ RT=3-x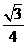 ×32
-
×32
- (3-x)2=
(3-x)2=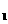 =1,x
=1,x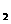 =5,因为0≤x≤3,所以x=1
=5,因为0≤x≤3,所以x=1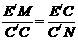 ∴C′N·E′M=C′C·E′C=
∴C′N·E′M=C′C·E′C= ×
×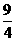
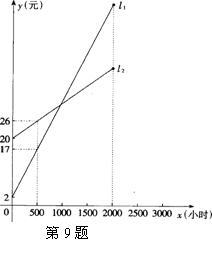 (2010 河南模拟)如图,
(2010 河南模拟)如图,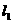 、
、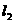 分别表示一种白炽灯和一种节能灯的费用
分别表示一种白炽灯和一种节能灯的费用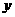 (费用=灯的售价+电费,单位:元)与照明时间
(费用=灯的售价+电费,单位:元)与照明时间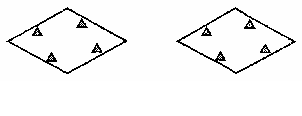 (2010 河南模拟)如图,菱形公园内有四个景点,请你用两种不同的方法,按下列要求设计成四个部分:⑴用直线分割;⑵每个部分内各有一个景点;⑶各部分的面积相等。(可用铅笔画,只要求画图正确,不写画法)
(2010 河南模拟)如图,菱形公园内有四个景点,请你用两种不同的方法,按下列要求设计成四个部分:⑴用直线分割;⑵每个部分内各有一个景点;⑶各部分的面积相等。(可用铅笔画,只要求画图正确,不写画法)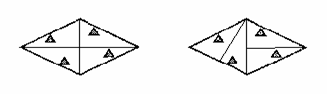
 (
(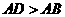 ),将纸片折叠一次,使点
),将纸片折叠一次,使点 与
与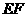 交
交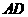 边于
边于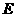 ,交
,交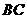 边于
边于 ,分别连结
,分别连结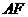 和
和 .
.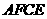 是菱形;
是菱形; ,
, 的面积为
的面积为 ,求
,求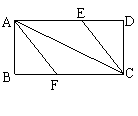 (3)在线段
(3)在线段 上是否存在一点
上是否存在一点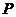 ,使得
,使得 ?若存在,请说明点
?若存在,请说明点 ,
,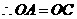 ,
,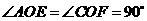
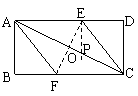
 在平行四边形
在平行四边形 ,
, ,
, .
.

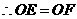 分
分 四边形
四边形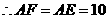 .
.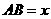 ,
,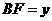 ,
,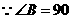 ,
,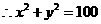
 ①
①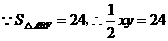 ,则
,则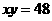 . ②
. ②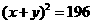
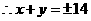 ,
, (不合题意舍去)
(不合题意舍去) 的周长为
的周长为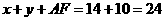 .
.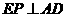 交
交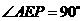 ,
,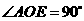 ,又
,又 ,
,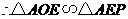 ,
,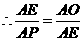 ,则
,则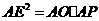
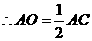 ,
, .
.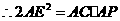
 (2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由。
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由。 cm,而制作这样的圆锥实际需要正方形纸片的对角线长为16+4+4
cm,而制作这样的圆锥实际需要正方形纸片的对角线长为16+4+4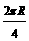
 cm,r=
cm,r=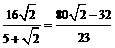 cm
cm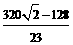 cm,底面圆的半径为
cm,底面圆的半径为 cm
cm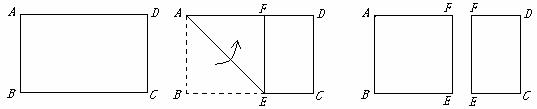
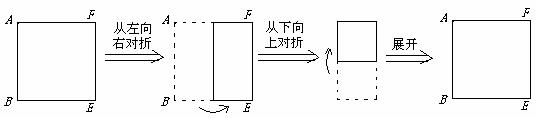
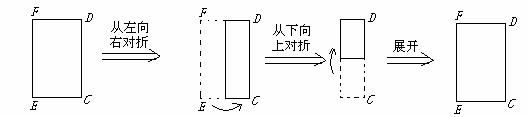
 (4)用(2)中所得到的两张纸片,分别裁剪出那两个四边形,用剩下的8张纸片拼出两个周长不相等的等腰梯形,用图表示并标明主要数据,分别求出两梯形的面积.
(4)用(2)中所得到的两张纸片,分别裁剪出那两个四边形,用剩下的8张纸片拼出两个周长不相等的等腰梯形,用图表示并标明主要数据,分别求出两梯形的面积. 

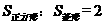 .
.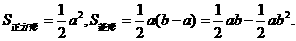
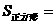
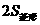 .
. ∴
∴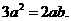
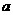 不等于0, ∴3
不等于0, ∴3 (4)如图所示。两等腰梯形周长分别为
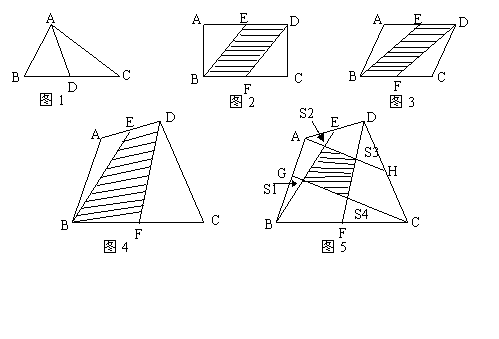
(4)如图所示。两等腰梯形周长分别为 .
.
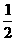 S矩形ABCD ,S阴=
S矩形ABCD ,S阴=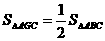 ,
,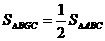
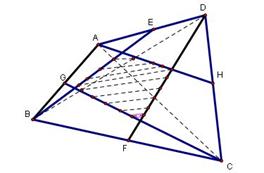 ∴
∴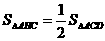 ,
,