⒈ 计算:sin300+cos600-cot2450-tan600tan300
⒉ 当x=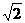 sin450+tan600时。先将代数式
sin450+tan600时。先将代数式 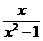 ÷(1+
÷(1+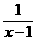 )化简后再求值。
)化简后再求值。
  A A D
D
B C 图19-7 |
⒊ 在Rt∆ABC中,∠C=900. a-b=2. tanA= 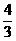 ,求a、b、c的值。
,求a、b、c的值。
⒋ 如图 19-7,已知∆ABC中,∠BAC=900.AB=AC. BD是AC边上的中线. 求cot∠DBC的值.
⒌ 在∆ABC中,已知BC=1+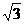 ∠B=600 ∠C=450.求AB的长.
∠B=600 ∠C=450.求AB的长.
 A
A  Q
Q B
P C B
P C图19-8 |
⒍ 身高相同的甲、乙、丙三人放风筝,各人放出的线分别为300m、250m、200m,线与平面所成的角分别为300、450、600(假定风筝线是拉直的)。问三人中谁放的风筝最高?
⒎ ∆ABC中,∠C=900,BC=8cm,sinB=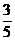 ,一只蜜蜂从点B开始沿BC向点C以2cm/s的速度移动。另一只蜜蜂从点C开始沿CA边向点A以1cm/s的速度移动。如果两只 蜜蜂分别从B、C点同时出发各自运动到P、Q,如图19-8,第几秒钟时PQ∥AB?
,一只蜜蜂从点B开始沿BC向点C以2cm/s的速度移动。另一只蜜蜂从点C开始沿CA边向点A以1cm/s的速度移动。如果两只 蜜蜂分别从B、C点同时出发各自运动到P、Q,如图19-8,第几秒钟时PQ∥AB?
第二课时(勾股定理、解直角三角形及有关知识解决实际问题)
课标要求
1、 熟悉勾股定理的探索过程,会用勾股定理解决简单的实际问题。
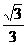
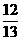 ,则 tanA等于(
).
,则 tanA等于(
).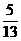 B.
B.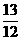 C.
C.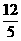 D.
D.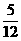
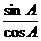 C.tanA=
C.tanA=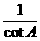 D.sin2600+sin2300=1
D.sin2600+sin2300=1 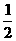 cos300+sin600cos60+
cos300+sin600cos60+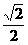 sin450=
sin450=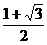 B.
B.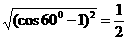
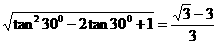
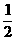 那么∆ABC是(
)
那么∆ABC是(
)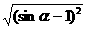 =1-sinα,正确的有( )
=1-sinα,正确的有( )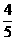 B.cosα=
B.cosα=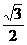 ) B.(-3,-
) B.(-3,- 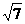 AB=3,则cosA=____________.
AB=3,则cosA=____________.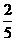 . AC=4. 则 BC=__________。
. AC=4. 则 BC=__________。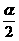 =______________
=______________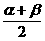 =___________
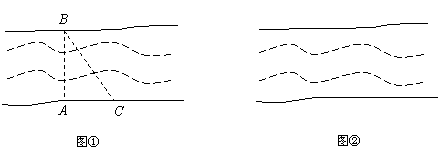
=___________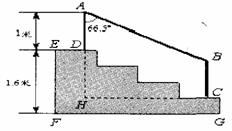 (2007苏州)某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为l.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66. 5°.
(2007苏州)某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为l.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66. 5°.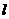 (即AD+AB+BC,结果精确到0.1米).(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
(即AD+AB+BC,结果精确到0.1米).(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)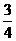 =l.2(米).(2)过B作BM⊥AH于M,则四边形BCHM是矩形.
=l.2(米).(2)过B作BM⊥AH于M,则四边形BCHM是矩形.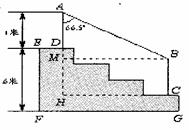 MH=BC=1 ∴AM=AH-MH=1+1.2一l=l.2.
MH=BC=1 ∴AM=AH-MH=1+1.2一l=l.2.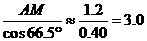 (米).
(米).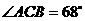 .
. 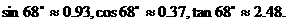 );
);
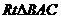 中,
中, (米)
(米)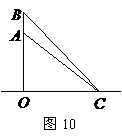 (2007贵州贵阳)如图10,一枚运载火箭从地面
(2007贵州贵阳)如图10,一枚运载火箭从地面 处发射,当火箭到达
处发射,当火箭到达 点时,从地面
点时,从地面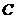 处的雷达站测得
处的雷达站测得 的距离是
的距离是 ,仰角是
,仰角是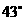 .
.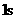 后,火箭到达
后,火箭到达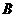 点,此时测得
点,此时测得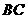 的距离是
的距离是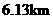 ,仰角为
,仰角为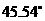 ,解答下列问题:
,解答下列问题: 中,
中,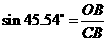 ····················· 1分
····················· 1分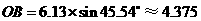 (km)······················ 3分
(km)······················ 3分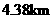 ············································································· 4分
············································································· 4分 中,
中,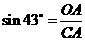 ············································································ 1分
············································································ 1分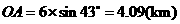 ························································································ 3分
························································································ 3分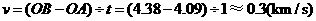 ······················································ 5分
······················································ 5分
 方向航行
方向航行 海里后到达
海里后到达 方向航行
方向航行 海里后到达
海里后到达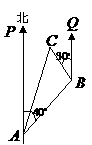 友情提示:以下数据可以选用:
友情提示:以下数据可以选用: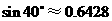 ,
,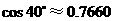 ,
,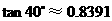 ,
,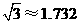 .
.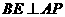 ,垂足为点
,垂足为点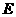 ;过
;过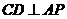 ,
,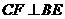 ,垂足分别为点
,垂足分别为点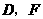 ,则四边形
,则四边形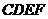 为矩形.
为矩形.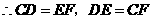 ,…………………………3分
,…………………………3分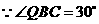 ,
,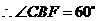 .
.
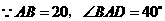 ,
,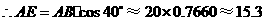 ;
;  .
. 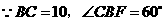 ,
,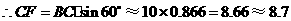 ;
;  .
. 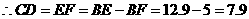 .
. 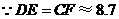 ,
,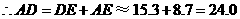 .
. 由勾股定理,得
由勾股定理,得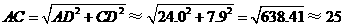 .
.