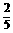36.在两个布袋中分别装有三个小球,这三个小球的颜色分别为红色、白色、绿色,其他没有区别.把两袋小球都搅匀后,再分别从两袋中各取出一个小球,试求取出两个相同颜色小球的概率(要求用树状图个或列表方法求解).
解:(解法一)


 列举所有等可能结果,画树状图:
列举所有等可能结果,画树状图:
 布袋1
红
白
绿
布袋1
红
白
绿
布袋2 红白绿 红白绿 红白绿
由上图2可知,所有等可能结果共有9种,两个相同颜色小球的结果共3种,
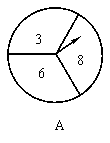
∴P(相同颜色)=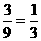
(解法二)列表如下:

|
红 |
白 |
绿 |
||||||
|
红 |
(红,红) |
(红,白) |
(红,绿) |
||||||
|
白 |
(白,红) |
(白,白) |
(白,绿) |
||||||
|
绿 |
(绿,红) |
(绿,白) |
(绿,绿) |
由上表可知,所有等可能结果共有9种,两个相同颜色小球的结果共3种,
∴P(相同颜色)=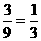
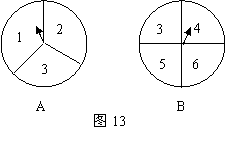
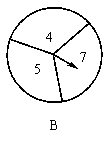
33.如图13,有两个可以自由转动的均匀转盘 .转盘
.转盘 被平均分成
被平均分成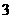 等份,分别标上
等份,分别标上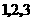 三个数字;转盘
三个数字;转盘 被平均分成4等份,分别标上
被平均分成4等份,分别标上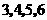 四个数字.有人为甲、乙两人设计了一个游戏规则;自由转动转盘
四个数字.有人为甲、乙两人设计了一个游戏规则;自由转动转盘 与
与 ,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则为乙获胜.
,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则为乙获胜.
 你认为这样的游戏规则是否公平?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方公平?
你认为这样的游戏规则是否公平?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方公平?
解:不公平.
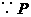 (和为6)
(和为6)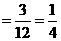 ,
,
甲、乙获胜的概率不相等
 不公平.
不公平.
规则改为:和是6或7,甲胜;否则乙胜.
(和为奇数,甲胜;和为偶数,乙胜;或和小于7,甲胜;和大于等于7,乙胜.答案不唯一.) 列 表
 B B |
3 |
4 |
5 |
6 |
|
1 |
4 |
5 |
6 |
7 |
|
2 |
5 |
6 |
7 |
8 |
|
3 |
6 |
7 |
8 |
9 |
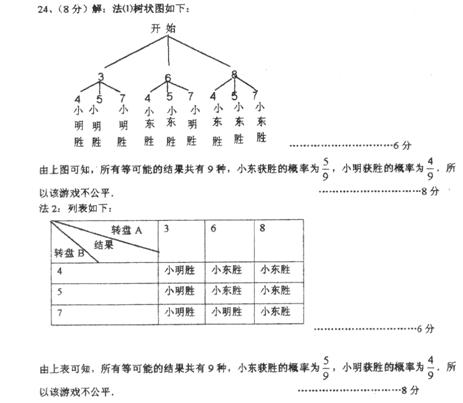
27.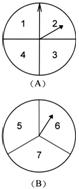 甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示. 游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示. 游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
解:⑴(法1)画树状图
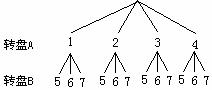
由上图可知,所有等可能的结果共有12种,指针所指的两个数字之和为奇数的结
果有6种. ∴P(和为奇数)=0.5
 (法2)列表如下:
(法2)列表如下:

|
1 |
2 |
3 |
4 |
||||||||||||||
|
5 |
1+5=6 |
2+5=7 |
3+5=8 |
4+5=9 |
||||||||||||||
|
6 |
1+6=7 |
2+6=8 |
3+6=9 |
4+6=10 |
||||||||||||||
|
7 |
1+7=8 |
2+7=9 |
3+7=10 |
4+7=11 |
由上表可知,所有等可能的结果共有12种,指针所指的两个数字之和为奇数的结
果有6种. ∴P(和为奇数)=0.5
⑵∵P(和为奇数)=0.5
∴P(和为偶数)=0.5
∴这个游戏规则对双方是公平的.
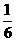
 、1、
、1、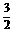 、2、
、2、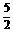 、3、
、3、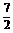 、4、
、4、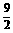 、5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1)、Q(x2,y2),则P、Q两点在同一反比例函数图象上的概率是( B )
、5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1)、Q(x2,y2),则P、Q两点在同一反比例函数图象上的概率是( B ) 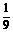 (B)
(B)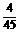 (C)
(C)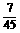 (D)
(D)