0 45663 45671 45677 45681 45687 45689 45693 45699 45701 45707 45713 45717 45719 45723 45729 45731 45737 45741 45743 45747 45749 45753 45755 45757 45758 45759 45761 45762 45763 45765 45767 45771 45773 45777 45779 45783 45789 45791 45797 45801 45803 45807 45813 45819 45821 45827 45831 45833 45839 45843 45849 45857 447348
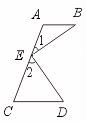
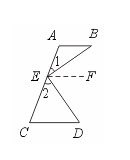 ∴ ∠BEF=∠B(两直线平行,内错角相等).
∴ ∠BEF=∠B(两直线平行,内错角相等).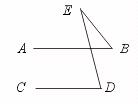
 证明:过点E作EF∥AB,
证明:过点E作EF∥AB,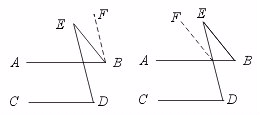
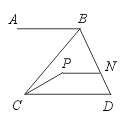
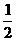 ∠BAC=
∠BAC=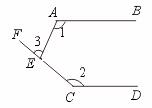
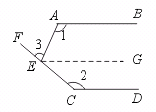
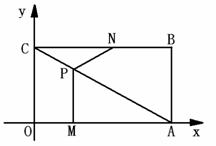
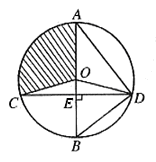
 的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。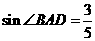 ,求CD的长;
,求CD的长;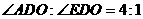 ,求扇形OAC(阴影部分)的面积(结果保留
,求扇形OAC(阴影部分)的面积(结果保留 )
)

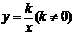 和一次函数
和一次函数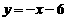 。
。