1.已知一次函数y = ax +b(a,b是常数),x与y的部分对应值如下表:
|
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
6 |
4 |
2 |
0 |
-2 |
-4 |
那么方程ax + b = 0的解是___________;不等式ax + b>0的解集是____________.
3.一次函数的运用
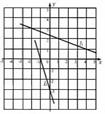 [例4] 如图,是在同一坐标系内作出的一次函数y1、y2的图象l1、l2,设y1=k1x+b1,y2=k2x+b2,则方程组的解是_______.
[例4] 如图,是在同一坐标系内作出的一次函数y1、y2的图象l1、l2,设y1=k1x+b1,y2=k2x+b2,则方程组的解是_______.
A、 B、
C、 D、
[例5] 在某地,人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表:
|
蟋蟀叫次数 |
… |
84 |
98 |
119 |
… |
|
温度(℃) |
… |
15 |
17 |
20 |
… |
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1分钟叫了63次,那么该地当时的温度大约为多少摄氏度?
[例6])某软件公司开发出一种图书管理软件,前期投入的开发、广告宣传费用共50000元,且每售出一套软件,软件公司还需支付安装调试费用200元.
(1)试写出总费用y(元)与销售套数x(套)之间的函数关系式;
(2)如果每套定价700元,软件公司至少要售出多少套软件才能确保不亏本?
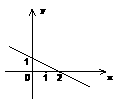
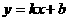 (
(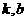 为常数)的图象如图所示,那么当
为常数)的图象如图所示,那么当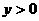 时,
时,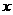 的取值范围是( )
的取值范围是( )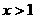 B、
B、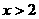 C、
C、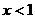 D、
D、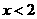
 [例1] 点A(2,4)在正比例函数的图象上,这个正比例函数的解析式是
[例1] 点A(2,4)在正比例函数的图象上,这个正比例函数的解析式是 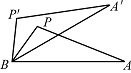 如图,如果△APB绕点B按逆时针方向旋转30°后得到
如图,如果△APB绕点B按逆时针方向旋转30°后得到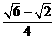 ,cos15°=
,cos15°=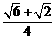 )
)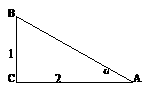
 中,
中,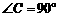 ,AB=15,sinA=,则BC等于( )
,AB=15,sinA=,则BC等于( )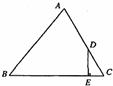 ⑥如图,在△ABC中,∠C=90º,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是( )
⑥如图,在△ABC中,∠C=90º,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是( )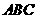 中,
中,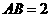 ,
,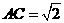 ,
,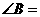 30º,则 ∠BAC 的度数是
.
30º,则 ∠BAC 的度数是
.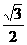 tan60°+|-2|+2-1.
tan60°+|-2|+2-1.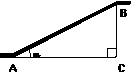 如图,等腰三角形ABC的顶角为1200,腰长为10,则底边上的高AD=
。
如图,等腰三角形ABC的顶角为1200,腰长为10,则底边上的高AD=
。