摘要： 反比例函数的应用 例31如图.点P是反比例函数y = 上的一点.PD⊥x轴于点D.则△POD的面积为 .
网址：http://m.1010jiajiao.com/timu3_id_454657[举报]
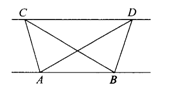
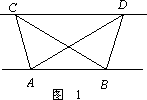
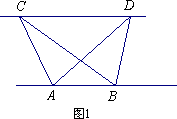
(1)如图，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由。
(2)结论应用：
①如图，点M，N在反比例函数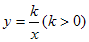
的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F。试证明：MN∥EF。
②若①中的其他条件不变，只改变点M，N的位置，如图所示。请判断MN与EF是否平行。
(2)结论应用：
①如图，点M，N在反比例函数
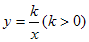的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F。试证明：MN∥EF。②若①中的其他条件不变，只改变点M，N的位置，如图所示。请判断MN与EF是否平行。
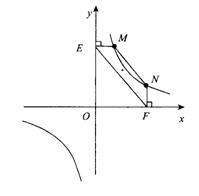
（2012•徐州）如图，直线y=x+b（b＞4）与x轴、y轴分别相交于点A、B，与反比例函数y=-
的图象相交于点C、D（点C在点D的左侧），⊙O是以CD长为半径的圆．CE∥x轴，DE∥y轴，CE、DE相交于点E．
（1）△CDE是
（2）b为何值时，点E在⊙O上？
（3）随着b取值逐渐增大，直线y=x+b与⊙O有哪些位置关系？求出相应b的取值范围．
查看习题详情和答案>>
| 4 |
| x |
（1）△CDE是
等腰直角
等腰直角
三角形；点C的坐标为（
，
）
-b-
| ||
| 2 |
b-
| ||
| 2 |
（
，
）
，点D的坐标为-b-
| ||
| 2 |
b-
| ||
| 2 |
（
，
）
-b+
| ||
| 2 |
b+
| ||
| 2 |
（
，
）
（用含有b的代数式表示）；-b+
| ||
| 2 |
b+
| ||
| 2 |
（2）b为何值时，点E在⊙O上？
（3）随着b取值逐渐增大，直线y=x+b与⊙O有哪些位置关系？求出相应b的取值范围．
(1)探究新知：
如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．
(2)结论应用：
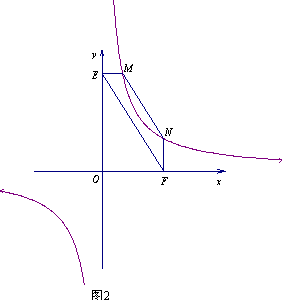
①如图2，点M，N在反比例函数
(k＞0)的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．
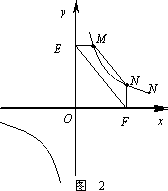
试证明：MN∥EF．
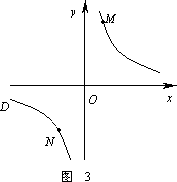
②若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断MN与EF是否平行．
的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．
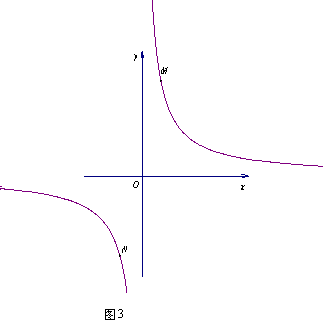
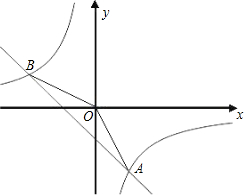其中A点的横坐标与B点的纵坐标都是2，如图：