摘要:(1)设为全集.是的三个非空子集.且.则下面论断正确的是 (A) (B) (C) (D) 解:∵所表示的部分是图中蓝色 的部分.所表示的部分是图中除去的部分. ∴.故选C. (2)一个与球心距离为1的平面截球所得的圆面面积为.则球的表面积为 (A) (B) (C) (D) 解:∵截面圆面积为.∴截面圆半径. ∴球的半径为. ∴球的表面积为.故选B. (3)函数.已知在时取得极值.则= 3 5 解:,令=0,解得a=5,选(D) (4)如图.在多面体ABCDEF中.已知ABCD是边长为1的正方形.且均为正三角形.EF∥AB.EF=2.则该多面体的体积为 (A) (B) (C) (D) 解:如图,过A.B两点分别作AM.BN垂直于EF.垂足分别为M.N.连结DM.CN.可证得DM⊥EF.CN⊥EF.多面体ABCDEF分为三部分.多面体的体积V为.∵..∴. 作NH垂直于点H.则H为BC的中点.则.∴.∴. ..∴.故选A. (5)已知双曲线的一条准线为.则该双曲线的离心率为 (A) (B) (C) (D) 解:由得.∴.抛物线的准线为.因为双曲线的一条准线与抛物线的准线重合.所以.解得.所以.所以离心率为.故选D. (6)当时.函数的最小值为 (A)2 (B) 解: .当且仅当.即时.取“ .∵.∴存在使.这时.故选(C). (7)反函数是 (A) (B) (C) (D) 解:由,得,故的反函数为,选(D) (8)设.函数.则使的的取值范围是 (A) (B) (C) (D) 解:∵..∴.解得 或. ∴.故选C. (9)在坐标平面上.不等式组所表示的平面区域的面积为 (A) (B) (C) (D)2 解:原不等式化为或. 所表示的平面区域如右图所示... ∴.故选B (10)在中.已知.给出以下四个论断: ① ② ③ ④ 其中正确的是 (A)①③ ①④ (D)②③ 解:∵.. ∴.∴. ∵.∴①不一定成立. ∵.∴.∴②成立. ∵.∴③不一定成立. ∵.∴④成立.故选B. (11)点O是三角形ABC所在平面内的一点.满足.则点O是的 (A)三个内角的角平分线的交点 (B)三条边的垂直平分线的交点 (C)三条中线的交点 (D)三条高的交点 解:,即 得, 即,故,,同理可证,∴O是的三条高的交点,选(D) (12)设直线过点.且与圆相切.则的斜率是 (A) (B) (C) (D) 解:设过点.且与圆相切的直线的斜率为k,则直线的方程为:y-kx+2k=0,k满足:1=得k=,选(D). 第Ⅱ卷
网址:http://m.1010jiajiao.com/timu3_id_4469201[举报]
设 为全集,
为全集,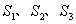 是
是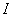 的三个非空子集,且
的三个非空子集,且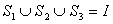 ,则下面论断正确的是
,则下面论断正确的是
(A)CI S1∩(S2∪S3)=Φ (B)S1![]() (CI S2∩CI S3)
(CI S2∩CI S3)
(C)CI S1∩CI S2∩CI S3=Φ (D)S1![]() (CI S2∪CI S3)
(CI S2∪CI S3)
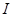 为全集,
为全集,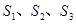 是
是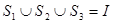 ,则下面论断正确的是 (
)
,则下面论断正确的是 (
) B
B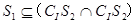
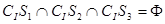 D
D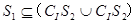 .
.