摘要:设函数(其中).且的图象在轴右侧的第一个最高点的横坐标为. (I)求的值. (II)如果在区间上的最小值为.求的值. 某大夏的一部电梯从底层出发后只能在第18.19.20层可以停靠.若该电梯在底层载有5位乘客.且每位乘客在这三层的每一层下电梯的概率均为.用表示这5位乘客在第20层下电梯的人数.求: (I)随机变量的分布列; (II)随机变量的期望; 如图.在四棱锥中.底面ABCD.为直角.,E.F分别为.中点. (I)试证:平面; (II)高.且二面角 的平面角大小.求的取值范围. 已知函数.其中为常数. (I)若.讨论函数的单调性, (II)若.且.试证: 已知定义域为R的函数满足 (I)若.求;又若.求; (II)设有且仅有一个实数.使得.求函数的解析表达式 已知一列椭圆.--.若椭圆上有一点.使到右准线的距离是与的等差中项.其中.分别是的左.右焦点. (I)试证:; (II)取.并用表示的面积.试证:且 普通高等学校招生全国统一考试 数学试题卷答案
网址:http://m.1010jiajiao.com/timu3_id_4468665[举报]
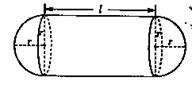
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为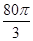 立方米,且
立方米,且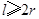 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为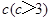 千元,设该容器的建造费用为
千元,设该容器的建造费用为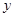 千元.
千元.
(Ⅰ)写出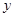 关于
关于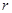 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的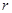 .
.
查看习题详情和答案>>
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为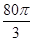 立方米,且
立方米,且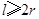 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为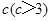 千元,设该容器的建造费用为
千元,设该容器的建造费用为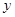 千元.
千元.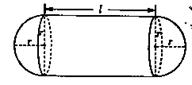
(Ⅰ)写出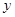 关于
关于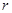 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的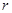 .
.
 ,其中
,其中 ,且a≠0.
,且a≠0. 在区间[1,e]上的最小值;
在区间[1,e]上的最小值; (其中
(其中 且
且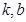 为常数)的图像经过点A
为常数)的图像经过点A 、B
、B .
. 是函数
是函数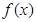 图像上的点,
图像上的点, 是
是 正半轴上的点.
正半轴上的点. 为坐标原点,
为坐标原点, 是一系列正三角形,记它们的边长是
是一系列正三角形,记它们的边长是 ,求数列
,求数列 的通项公式;
的通项公式; 满足
满足 ,记
,记 项和为
项和为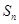 ,证明:
,证明: 。
。 ax2+3x.
ax2+3x.