0 446413 446421 446427 446431 446437 446439 446443 446449 446451 446457 446463 446467 446469 446473 446479 446481 446487 446491 446493 446497 446499 446503 446505 446507 446508 446509 446511 446512 446513 446515 446517 446521 446523 446527 446529 446533 446539 446541 446547 446551 446553 446557 446563 446569 446571 446577 446581 446583 446589 446593 446599 446607 447348
 方程为
方程为 ,设点
,设点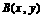 ,由
,由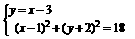 及
及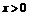 ,
,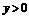 得
得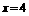 ,
,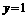 ,点
,点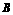 的坐标为
的坐标为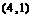 。
。 得
得 ,设
,设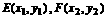 ,则
,则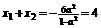 ,得
,得 。
。 坐标为
坐标为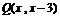 ,
,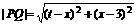 ,
,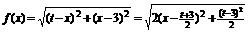
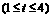 ,
, 时,即
时,即 时,
时,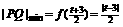 ,
, ,即
,即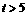 时,
时, 在
在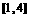 上单调递减,∴
上单调递减,∴ ;
; 当
当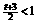 ,即
,即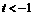 时,
时,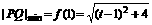 。
。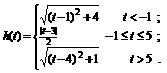
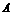 、
、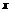 轴于
轴于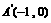 、
、 ,
, 在线段
在线段 上,即
上,即 时,由点到直线的距离公式得:
时,由点到直线的距离公式得: ;
; 的左边,
的左边, ;
;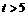 时,
时,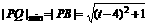 。
。 的直线
的直线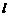 过点
过点 和点
和点 ,
, .
.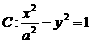
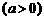 相交于
相交于 、
、 两点,且线段
两点,且线段 的中点坐标为
的中点坐标为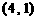 ,求
,求 的值;
的值;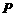 ,当点
,当点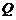 在线段
在线段 上运动时,称
上运动时,称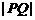 的最小值为
的最小值为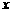 轴上运动,写出点
轴上运动,写出点 到线段
到线段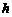 关于
关于 的函数关系式.
的函数关系式.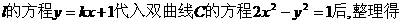
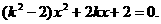 ……①
……①
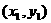 、
、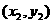 ,则由①式得
,则由①式得 ……②
……②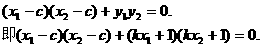
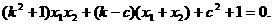 ……③
……③ 代入③式化简得
代入③式化简得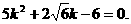

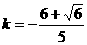 使得以线段AB为直径的圆经过双曲线C的右焦点
使得以线段AB为直径的圆经过双曲线C的右焦点 的右支交于不同的两点A、B.
的右支交于不同的两点A、B. x2,
①
x2,
①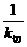 =-
=-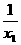 ,
,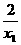 x-x12-2=0.
x-x12-2=0.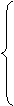 x0=
x0=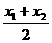 =-
=-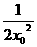 +1(x0≠0),
+1(x0≠0), =kl=-
=kl=- ,
,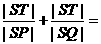
 .
.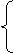 y=
y=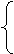 y1+y2=2(k2+b),
y1+y2=2(k2+b), )≥2|b|
)≥2|b|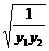 =2|b|
=2|b|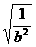 =2.
=2.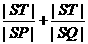 的取值范围是(2,+
的取值范围是(2,+ ).
). =|b|
=|b| .
. =
=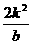 +2>2;
+2>2; .
.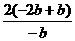 =2.
=2. =
=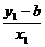 .
.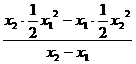 =-
=- =
= +
+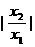 +
+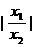 ≥2.
≥2.
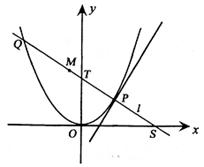 (Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求
(Ⅱ)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求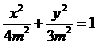
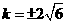 或0
或0 与y轴交于点M. 若
与y轴交于点M. 若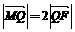 ,求直线
,求直线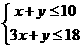 ,设
,设
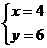 时,
时, 取最大值7万元
取最大值7万元