摘要: 已知函数f(x-2)=ax2-(a-3)x+a-2(a<0,a∈Z)的图象与x轴有交点. (1)求a的值,(2)求f(x)的解析式, (3)若g(x)=1-[f(x)]2,F(x)=c·g(x)+d·f(x).问是否存在c(c>0).d使得在区间(-∞,f(2))内是单调递增函数.而在区间(f内是单调递减函数?若存在.求c,d之间的关系.并写出推理过程,若不存在.说明理由. 解: (1)a=-1; (2)f(x)=-x2+1 (3)g(x)=-x4+2x2,F(x)=-cx4+(2c-d)x2+d(c>0). 若F(x)在(-∞,f上为增函数.则当x1<x2<-3时F(x2)-F(x1)>0,于是有(x22-x12)[-c(x12+x22)+2c-d]>0. ∵x22-x12<0,∴-c(x12+x22)+2c-d<0. ∴x12+x22>. 要使该式在上恒成立.只须≤(-3)2+(-3)2=18,即16c+d≥0,同样的方法可得.要使F(x)在上为减函数.只须16c+d≤0,因此当16c+d=0时满足给出的所有条件. 另解:依题意.F(x)在x=-3时有极大值. ∵F′(x)=-4cx3+2(2c-d)x, ∴F′(x)|x=-3=0,同样可得16c+d=0.
网址:http://m.1010jiajiao.com/timu3_id_4464043[举报]
本小题满分12分)
已知 函数f (x)=
函数f (x)= x3+ ax2-bx (a, b∈R) .
x3+ ax2-bx (a, b∈R) .
(1)若y=f (x)图象上的点(1,- )处的切线斜率为-4
)处的切线斜率为-4 ,求y=f (x)的极大值;
,求y=f (x)的极大值;
(2)若y=f (x)在区间[-1,2]上是单调减函数,求a + b的最小值.
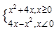 (1)作出函数
(1)作出函数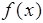 的图像简图,并指出函数
的图像简图,并指出函数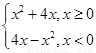
 的图像简图,并指出函数
的图像简图,并指出函数