摘要: 直线l:y=mx+1与椭圆C:ax2+y2=2交于A.B两点.以OA.OB为邻边作平行四边形OAPB(O为坐标原点) (1)当a=2时.求点P的轨迹方程, (2)当a,m满足a+2m2=1.且记平行四边形OAPB的面积函数S(a),求证:2<S(a)<4. (1)解:设P(x,y).则OP中点为E() 由消去y得(2+m2)x2+2mx-1=0设A(x1,y1),B(x2,y2) 则=-,=m+1= 即AB的中点为E(-,) 于是 消去m,得点P的轨迹方程为2x2+y2-2y=0 (2)证明:由消去y得(a+m2)x2+2mx-1=0进一步就可以求出|AB|= ∵O到AB的距离d=·S(a)=|AB|d= ∵a+2m2=1∴0<a<1∴2<S(a)<4
网址:http://m.1010jiajiao.com/timu3_id_4464041[举报]
 ,直线l与圆C总有两个不同的交点。
,直线l与圆C总有两个不同的交点。 ,求l的倾斜角;
,求l的倾斜角;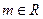 ,直线l与圆C总有两个不同的交点。
,直线l与圆C总有两个不同的交点。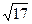 ,求l的倾斜角;
,求l的倾斜角;