(1)记有限元素集合A的元素个数为n(A),A ={1,2,3}时,n(A)=3,若I是全集,M、N是其子集,且n(Ⅰ)=8,n( ∩N)=3,n(M∩N)=1,n(
∩N)=3,n(M∩N)=1,n( ∩
∩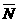 )=2,则n(M)=
)=2,则n(M)=
(A)4 (B)3 (C)2 (D)1
(2)若函数y =f(x)的图象和y =sin(x+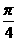 )的图象关于点A(
)的图象关于点A(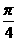 ,0)对称,则f(x)的表达式是
,0)对称,则f(x)的表达式是
(A)cos(x+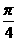 ) (B)-cos(x-
) (B)-cos(x-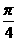 )
)
(C)-cos(x+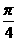 ) (D)cos(x-
) (D)cos(x-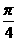 )
)
(3)一个圆锥的侧面展开图扇形的周长为2,则这个圆锥侧面积的最大值是
(A)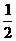 (B)
(B)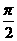 (C)
(C)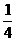 (D)
(D)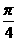
(4)如图,虚线部分是四个象限的角平分线,实线部分是函数y=f(x)的图象,则f(x)只能是
(A) 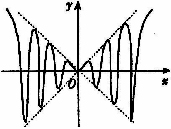 xsin
xsin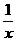
(B) xcos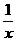
(C) x2sin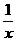
(D)x2cos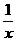
(5)在一定的条件下,某种细胞经过1小时1个分裂为2个,已知一定数量的细胞经过20个小时的分裂,细胞的个数成为230个,那么分裂到215个细胞需要
(A)1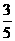 小时 (B)5小时 (C)2小时 (D)1
小时 (B)5小时 (C)2小时 (D)1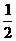 小时
小时
(6)在△ABC中,a2+b2=d·c2,且ctgC=1000(ctgA+ctgB),则常数d的值等于
(A)1999 (B)2000 (C)2001 (D)2002
(7)已知圆(x-3)2+(y+4)2=r2上至多有两点到直线4x -3y –4 = 0的距离为1,则半径r的取值范围是
(A)(0,4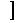 (B)(0,5) (C)(0,5
(B)(0,5) (C)(0,5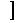 (D)[5,+∞]
(D)[5,+∞]
(8)某公司从2000年起,每人的年工资由三个项目组成并按下表规定实施
|
项目 |
计算办法 |
|
基础工资 |
2000年1万元,考虑物价因素,以后每年递增10% |
|
住房补贴 |
按工龄计算:400元×工龄(工龄计算方法,如某职工1998年进公司,到2001年按4年计算) |
|
医疗费 |
每年1600元,固定不变 |
该公司的一职工在2002年将得到的住房补贴和医疗费之和可超过基础工资的25%,这位职工的工龄至少是
(A)2年 (B)3年 (C)4年 (D)5年
(9)设Sn为等差数列{an}的前n项和,S9=18,an-4=30(n>9),Sn=336,则n的值为
(A)16 (B)21 (C)2 (D)18
(10)若不等式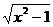 ≤
≤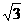 ax的解集为{x|1≤x≤2},则实数a的取值集合为
ax的解集为{x|1≤x≤2},则实数a的取值集合为
(A){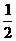 } (B){1} (C){a|a>4} (D){a|a>
} (B){1} (C){a|a>4} (D){a|a>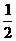 }
}
(11)对于函数f(x),在同一坐标系中,y1=f(x-19)与y2=f(99-x)的图象恒关于( )对称
(A)y轴 (B)直线x =19 (C)直线x =59 (D)直线x =99
(12)函数f(x)=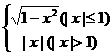 ,如果方程f(x)=a有且只有一个实根,那么a满足
,如果方程f(x)=a有且只有一个实根,那么a满足
(A)a<0 (B)0≤a<1 (C)a=1 (D)a>1
21、 (本小题满分12分)
(本小题满分12分)
如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,线段OD的中垂线与半圆交于E、F两点,已知|AB|=4,曲线C过E点,动点P在曲线C上运动且保持||PA|-|PB||的值不变。
(1)建立适当的平面直角坐标系, D

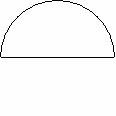 求曲线C的方程;
求曲线C的方程;
 (2)过D点的直线
(2)过D点的直线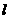 与曲线C相交
E
F
与曲线C相交
E
F
|
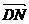 =3
=3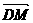 ,
A
B
,
A
B
求直线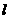 的方程。
的方程。
19、(本小题满分12分)
如图,在四棱锥P-ABCD中,PA、AB、AD

|
|
|





|

 两两互相垂直,AB∥CD,且AB=1,AD=CD=2,
两两互相垂直,AB∥CD,且AB=1,AD=CD=2,
|
(1)求证:BE∥平面PAD;
(2)当平面PCD与平面ABCD成多大角时,
BE⊥平面PCD;
|
求四棱锥P-ABCD的体积。
 (15)等比数列{an}的前n项和Sn=r-(
(15)等比数列{an}的前n项和Sn=r-( [f(x)-f(-x)],是否存在自然数m和M,使不等式m<g(
[f(x)-f(-x)],是否存在自然数m和M,使不等式m<g( =(cosα,sinα),
=(cosα,sinα), 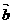 =(cosβ,sinβ)
=(cosβ,sinβ)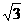 |
|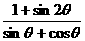 的值域。
的值域。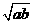 ;
②sin2x+
;
②sin2x+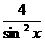 ≥4;
≥4;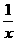 +
+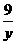 =1,则x+y的最小值是12;
=1,则x+y的最小值是12;