0 446151 446159 446165 446169 446175 446177 446181 446187 446189 446195 446201 446205 446207 446211 446217 446219 446225 446229 446231 446235 446237 446241 446243 446245 446246 446247 446249 446250 446251 446253 446255 446259 446261 446265 446267 446271 446277 446279 446285 446289 446291 446295 446301 446307 446309 446315 446319 446321 446327 446331 446337 446345 447348
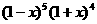 的展开式中
的展开式中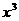 的系数是( )
的系数是( )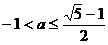 . 15、
. 15、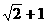 4 . 16、1/2 .
4 . 16、1/2 .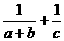 的最小值为 .
的最小值为 .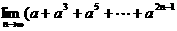 )≤1,则a =
.
)≤1,则a =
.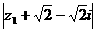 ≤1,复数z2满足
≤1,复数z2满足 那么|z1-z2|的最小值为
.
那么|z1-z2|的最小值为
.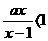 的解集为{x|x<1或x>2=,那么a的值为
的解集为{x|x<1或x>2=,那么a的值为 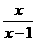 (D)y
=
(D)y
=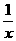
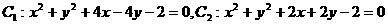 相交于P、Q两点,则下列各点在弦PQ所在直线上的是
相交于P、Q两点,则下列各点在弦PQ所在直线上的是 的图象上各点的横坐标扩大到原来的3倍,纵坐标也扩大到原来的3倍,则所得图象的解析式为
的图象上各点的横坐标扩大到原来的3倍,纵坐标也扩大到原来的3倍,则所得图象的解析式为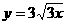 (B)
(B) 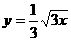 (C)
(C) 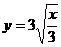 (D)
(D) 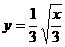
 +
+ ,则
,则 α,a⊥b,则α⊥β;(2)若α⊥β,α∩γ=a,β∩γ=b,则a⊥b;(3)若a不垂直于平面α,则a不可能垂直于α内的无数条直线;(4)若a⊥α,b⊥β,a∥b,则α∥β,其中不正确命题的个数为
α,a⊥b,则α⊥β;(2)若α⊥β,α∩γ=a,β∩γ=b,则a⊥b;(3)若a不垂直于平面α,则a不可能垂直于α内的无数条直线;(4)若a⊥α,b⊥β,a∥b,则α∥β,其中不正确命题的个数为
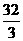 (B)
(B)
 (C)
(C)
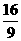 (D)
(D)
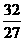
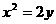 上距离点A(0,a)(a>0)最近的点恰好是顶点,这个结论成立的充要条件是
上距离点A(0,a)(a>0)最近的点恰好是顶点,这个结论成立的充要条件是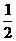 (D)0<a≤1
(D)0<a≤1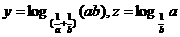 ,则x、y、z之间的大小关系为
,则x、y、z之间的大小关系为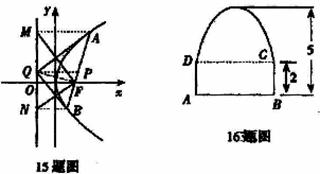
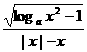 ,a>1},则
,a>1},则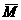 等于
等于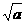 )
(B)[-
)
(B)[-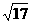 (B)
(B) 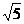 (C)2
(C)2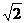
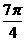 )的圆的方程是
)的圆的方程是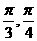 ,]上递增,那么
,]上递增,那么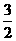 (B)0<ω≤2 (C)0<ω≤
(B)0<ω≤2 (C)0<ω≤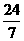 (D)ω≥2
(D)ω≥2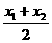 )>
)> [f(x1)+f(x2)],则f(x)在[a,b]上是上凸函数,在以下图象中,是上凸函数的图象是
[f(x1)+f(x2)],则f(x)在[a,b]上是上凸函数,在以下图象中,是上凸函数的图象是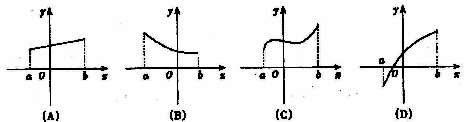
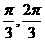 ,),则f(x)的值域是
,),则f(x)的值域是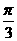 ,π)
(B)(-
,π)
(B)(-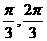 )
(D)(
)
(D)(  的值是 (A)
的值是 (A)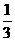 (C)2 (D)1
(C)2 (D)1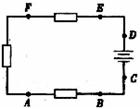 (A)1
(B)2
(C)3
(D)4
(A)1
(B)2
(C)3
(D)4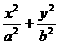 =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为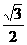 (B)
(B) 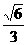 (C)
(C) 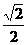 (D)
(D) 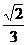
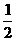 的是
的是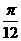 -1
-1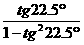 (D)
(D)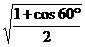
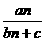 ,其中a,b,c均为正数,那么an与
,其中a,b,c均为正数,那么an与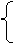 x=rsinθ
x=rsinθ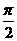 )所表示的图形是
)所表示的图形是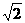 ∶
∶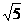 (D)2∶
(D)2∶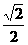 (B)
(B)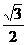 (C)2-
(C)2-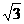 (D)
(D)
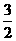 ) (D)(-
) (D)(- ,1) (B)(0,
,1) (B)(0,