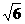6.二面角α-a-β的平面角为120°,在面α内,AB⊥a于B,AB=2在平面β内,CD⊥a于D,CD=3,BD=1,M是棱a上的一个动点,则AM+CM的最小值为 (C)
A.2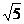 B.2
B.2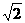 C.
C. D.2
D.2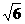
6.二面角α-a-β的平面角为120°,在面α内,AB⊥a于B,AB=2在平面β内,CD⊥a于D,CD=3,BD=1,M是棱a上的一个动点,则AM+CM的最小值为 (C)
A.2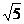 B.2
B.2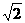 C.
C. D.2
D.2