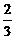1.已知点A、B、C、D的坐标分别为(-1,0,1),(0,0,1),(2,2,2)(0,0,3),则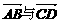 所成的角为
所成的角为
A.arccos(-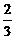 ) B.-arccos(-
) B.-arccos(-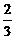 )
)
C.arccos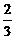 D.-arccos
D.-arccos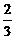
1.已知点A、B、C、D的坐标分别为(-1,0,1),(0,0,1),(2,2,2)(0,0,3),则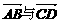 所成的角为
所成的角为
A.arccos(-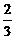 ) B.-arccos(-
) B.-arccos(-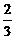 )
)
C.arccos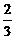 D.-arccos
D.-arccos