0 445890 445898 445904 445908 445914 445916 445920 445926 445928 445934 445940 445944 445946 445950 445956 445958 445964 445968 445970 445974 445976 445980 445982 445984 445985 445986 445988 445989 445990 445992 445994 445998 446000 446004 446006 446010 446016 446018 446024 446028 446030 446034 446040 446046 446048 446054 446058 446060 446066 446070 446076 446084 447348
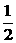 D.
D.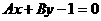 在y轴上的截距是-1,且它的倾斜角是直线
在y轴上的截距是-1,且它的倾斜角是直线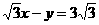 的倾斜角的2倍,则 ( )
的倾斜角的2倍,则 ( )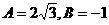 B.
B.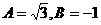 C.
C.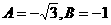 D.
D.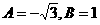
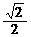 B.
B.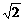 C.2 D.
C.2 D.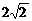
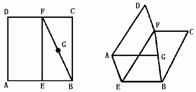
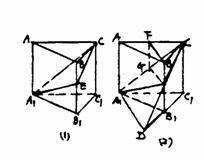
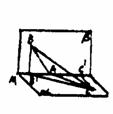
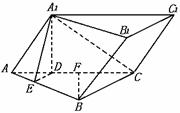
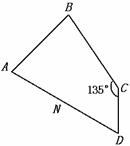
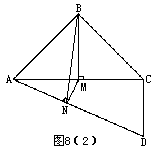
 ,求二面角C-AD-B的大小及三棱锥C-ABD的体积。
,求二面角C-AD-B的大小及三棱锥C-ABD的体积。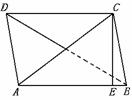
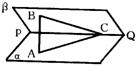
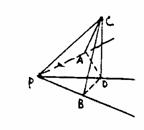
 ,P、Q两点分别在线段BD和SC上 ,则P、Q两点的最短距离为
.
,P、Q两点分别在线段BD和SC上 ,则P、Q两点的最短距离为
. (2)
(2) 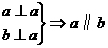
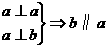 (4)
(4)
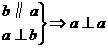
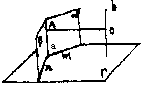
 α,m
α,m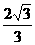 B.
B.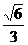 C.
C.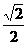 D.
D.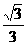
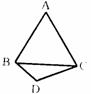
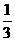 B.
B.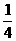 C.
C.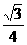 D.
D.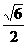 D.arccos
D.arccos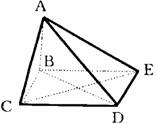
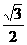 D.
D.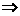 D.错误
D.错误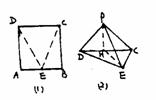
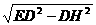
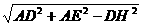 =l,
=l,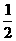 .
.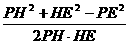
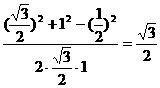 ,
,
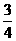 B.
B.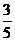 C.
C.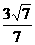 D.
D.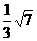
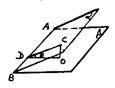
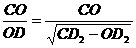
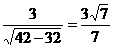 .
.

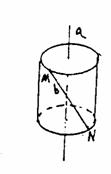
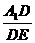 =
=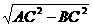 =2
=2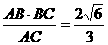

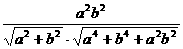 .
.
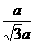 =
=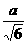 ,MB=
,MB=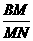 =
=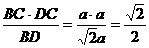 a,故C到平面ABD的距离为
a,故C到平面ABD的距离为