摘要：(三)解答题 16.已知平面α和不在这个平面内的直线a都垂直于平面β.求证a∥α. 17.如图.正方形ABCD.E.F分别在AB.CD的中点.G为BF的中点.现将正方形沿EF折成 120°的二面角.求①异面直线EF和AG所成的角,②AG和平 面EBCF所形成的角. 18.圆柱底面半径是3.高是4.A与B分别是两底的圆周上的点.且AB＝5.求异面直线AB与OO 1间的距离. 19.如图.已知二面角α-PQ-β为60°.点A和B分别在平面α和平面β内.点C在棱PQ 上.且∠ACP=∠BCP=30°AC=BC ①求证AB⊥PQ,②求直线PQ 在面ABC所成角的大小. 20.如图.设ABCD是矩形.沿对角线DB将ABDC折起.使点C在底面DAB上的射影E恰好落在 AB边上 (1)求证:平面ABC⊥平面ACD. (2)若AB＝2.BC＝.求二面角C-AD-B的大小及三棱锥C-ABD的体积.
网址：http://m.1010jiajiao.com/timu3_id_4459878[举报]
．三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数
为偶函数， 且
（1）求
的值；
（2）若
为三角形
的一个内角，求满足
的的值.
查看习题详情和答案>>
．三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数
为偶函数， 且
（1）求
的值；
（2）若
为三角形
的一个内角，求满足
的的值.
三、解答题：（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．）
16. （本小题满分12分）
已知向量
，定义函数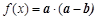
（Ⅰ）求函数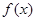
最小正周期；
（Ⅱ）在△ABC中,角A为锐角，且
，求边AC的长．
查看习题详情和答案>>
16．(本小题满分12分)[来源:学§科§网]
．
的解析式；
，且
，
的值．
，定义函数
最小正周期；
，求边AC的长．