摘要:(九)点到直线.点到平面.直线与平面.平面与平面间的距离的定义及计算 例9 已知Rt△ABC中.∠A=90°.AB=a.AC=b.沿高AD折成直二面角判断此时△ABC的形状,(2)求D到平面ABC的距离. 解:(1)DH⊥平面ABC.因DA.DB.DC两两互相垂直.故H为△ABC的垂心.AE⊥BC.由cosθ=cosθ1cosθ2.得cos∠ABE=cos∠ABD ·cos∠DBC. ∵∠ABD和∠DBC分别为Rt△BDC的锐角.故0<cos∠ABD.cos∠DBC<1. ∴0<cos∠ABE<1.即∠ABC为锐角. 同理可证∠ABC.∠CAB均为锐角.∴△ABC为锐角三角形. (2)解法一:设D到平面ABC的距离为x.∵VD-ABC=VA-BDC得xSABC=AD·S△BDC. 解出 x=. 解法二:作AE⊥BC.AD⊥平面DBC.故DE⊥BC.BC⊥平面ADE.平面ADE⊥平面ABC.作DH⊥AE .则DH是D到平面ABC的距离(以点线距离代替点面距离).在Rt△ADE中.DH是斜边AE上的高.解出 DH=.
网址:http://m.1010jiajiao.com/timu3_id_4459872[举报]
 (2012•奉贤区一模)出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的.在出租车几何学中,点还是形如(x,y)的有序实数对,直线还是满足ax+by+c=0的所有(x,y)组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点A(x1,y1),B(x2,y2)定义它们之间的一种“距离”:|AB|=|x1-x2|+|y1-y2|,请解决以下问题:
(2012•奉贤区一模)出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的.在出租车几何学中,点还是形如(x,y)的有序实数对,直线还是满足ax+by+c=0的所有(x,y)组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点A(x1,y1),B(x2,y2)定义它们之间的一种“距离”:|AB|=|x1-x2|+|y1-y2|,请解决以下问题:(1)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(2)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆周”上的所有点到点Q(a,b)的“距离”均为 r的“圆”方程;
(3)点A(1,3)、B(6,9),写出线段AB的垂直平分线的轨迹方程并画出大致图象.(说明所给图形小正方形的单位是1)
(2012•奉贤区一模)出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的.在出租车几何学中,点还是形如(x,y)的有序实数对,直线还是满足ax+by+c=0的所有(x,y)组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点A(x1,y1),B(x2,y2)定义它们之间的一种“距离”:|AB|=|x1-x2|+|y1-y2|,请解决以下问题:
(1)求点A(1,3)、B(6,9)的“距离”|AB|;
(2)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(3)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点A(1,3)、B(6,9),C(1,9),求经过这三个点确定的一个“圆”的方程,并画出大致图象;(说明所给图形小正方形的单位是1)

查看习题详情和答案>>
(1)求点A(1,3)、B(6,9)的“距离”|AB|;
(2)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(3)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点A(1,3)、B(6,9),C(1,9),求经过这三个点确定的一个“圆”的方程,并画出大致图象;(说明所给图形小正方形的单位是1)

、出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的。在出租车几何学中,点还是形如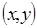 的有序实数对,直线还是满足
的有序实数对,直线还是满足 的所有
的所有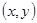 组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点 定义它们之间的一种“距离”:
定义它们之间的一种“距离”: ,请解决以下问题:
,请解决以下问题:
1、(理)求线段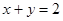
 上一点
上一点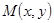 的距离到原点
的距离到原点 的“距离”;
的“距离”;
(文)求点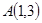 、
、 的“距离”
的“距离” ;
;
2、(理)定义:“圆”是所有到定点“距离”为定值的点组成的图形,
求“圆周”上的所有点到点 的“距离”均为
的“距离”均为 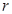 的“圆”方程;
的“圆”方程;
(文)求线段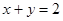
 上一点
上一点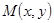 的距离到原点
的距离到原点 的“距离”;
的“距离”;
3、(理)点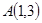 、
、 ,写出线段
,写出线段 的垂直平分线的轨迹方程并画出大致图像.
的垂直平分线的轨迹方程并画出大致图像.
(文)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点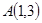 、
、 ,
, ,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
(说明所给图形小正方形的单位是1)

查看习题详情和答案>>
出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的.在出租车几何学中,点还是形如(x,y)的有序实数对,直线还是满足ax+by+c=0的所有(x,y)组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点A(x1,y1),B(x2,y2)定义它们之间的一种“距离”:|AB|=|x1-x2|+|y1-y2|,请解决以下问题:
(1)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(2)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆周”上的所有点到点Q(a,b)的“距离”均为 r的“圆”方程;
(3)点A(1,3)、B(6,9),写出线段AB的垂直平分线的轨迹方程并画出大致图象.(说明所给图形小正方形的单位是1)
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(2)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆周”上的所有点到点Q(a,b)的“距离”均为 r的“圆”方程;
(3)点A(1,3)、B(6,9),写出线段AB的垂直平分线的轨迹方程并画出大致图象.(说明所给图形小正方形的单位是1)
 查看习题详情和答案>>
查看习题详情和答案>>
出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的.在出租车几何学中,点还是形如(x,y)的有序实数对,直线还是满足ax+by+c=0的所有(x,y)组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点A(x1,y1),B(x2,y2)定义它们之间的一种“距离”:|AB|=|x1-x2|+|y1-y2|,请解决以下问题:
(1)求点A(1,3)、B(6,9)的“距离”|AB|;
(2)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(3)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点A(1,3)、B(6,9),C(1,9),求经过这三个点确定的一个“圆”的方程,并画出大致图象;(说明所给图形小正方形的单位是1)

查看习题详情和答案>>
(1)求点A(1,3)、B(6,9)的“距离”|AB|;
(2)求线段x+y=2(x≥0,y≥0)上一点M(x,y)的距离到原点O(0,0)的“距离”;
(3)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点A(1,3)、B(6,9),C(1,9),求经过这三个点确定的一个“圆”的方程,并画出大致图象;(说明所给图形小正方形的单位是1)

查看习题详情和答案>>