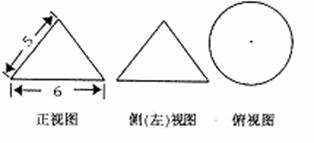
 13.一个几何体的三视图及其尺寸如下(单位:㎝),则该几何体的表面积是
,体积是
.
13.一个几何体的三视图及其尺寸如下(单位:㎝),则该几何体的表面积是
,体积是
.
|
14.将正奇数按一定规律填在5列的数表中,
则第252行,第3列的数是 .
 13.一个几何体的三视图及其尺寸如下(单位:㎝),则该几何体的表面积是
,体积是
.
13.一个几何体的三视图及其尺寸如下(单位:㎝),则该几何体的表面积是
,体积是
.
|
14.将正奇数按一定规律填在5列的数表中,
则第252行,第3列的数是 .