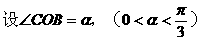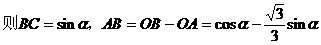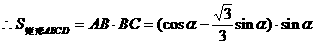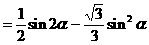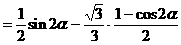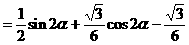0 445946 445954 445960 445964 445970 445972 445976 445982 445984 445990 445996 446000 446002 446006 446012 446014 446020 446024 446026 446030 446032 446036 446038 446040 446041 446042 446044 446045 446046 446048 446050 446054 446056 446060 446062 446066 446072 446074 446080 446084 446086 446090 446096 446102 446104 446110 446114 446116 446122 446126 446132 446140 447348
 x的取值范围是( )
x的取值范围是( )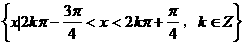
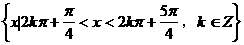
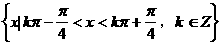
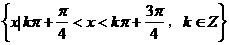
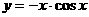 的部分图象是( )
的部分图象是( )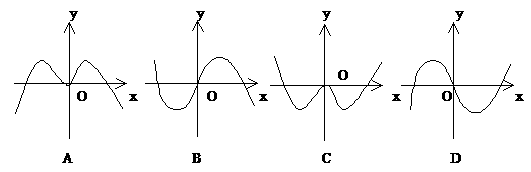
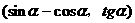 在第一象限,则在[0,2
在第一象限,则在[0,2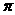 ]内
]内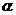 的取值范围是( )
的取值范围是( )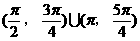
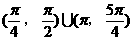
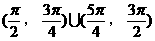
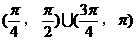
 的最小值为( )
的最小值为( )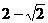 B.
B.
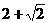
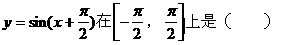
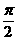 为周期的函数是( )
为周期的函数是( )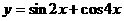
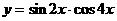
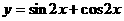
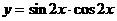
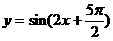 的图象的一条对称轴方程是( )
的图象的一条对称轴方程是( )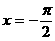 B.
B.
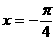
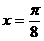 D.
D.
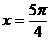
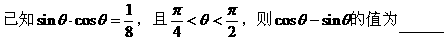
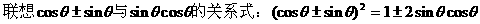
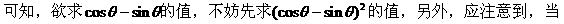
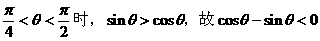
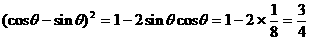
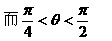
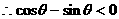
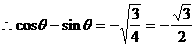
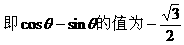
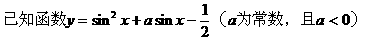
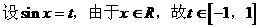
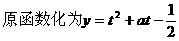
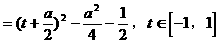
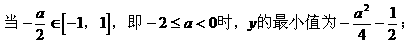

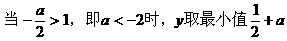
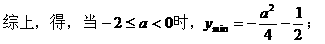
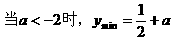
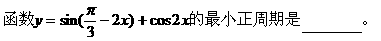
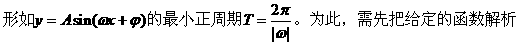 式通过三角公式,变形为上述结论中的函数形式,于是:
式通过三角公式,变形为上述结论中的函数形式,于是: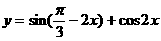
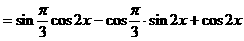
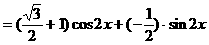
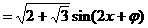
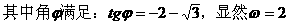

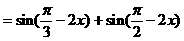
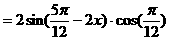
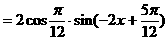
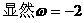

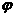 )的形式,在求其最小正周期时,往往先将解析式变形为y=Asin(ωx+
)的形式,在求其最小正周期时,往往先将解析式变形为y=Asin(ωx+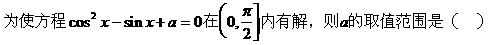




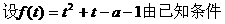
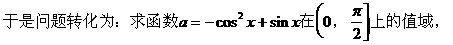
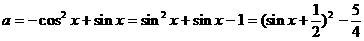
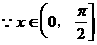
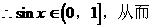
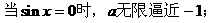
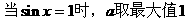
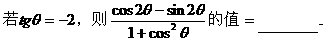
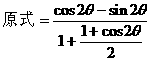
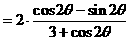
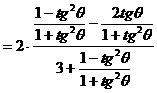
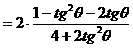
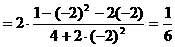
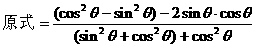
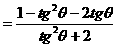
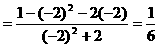
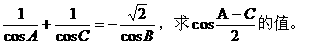
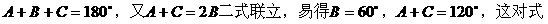

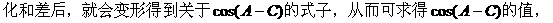
 的式子,从而立即求值。
的式子,从而立即求值。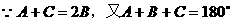
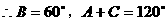
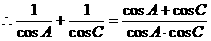
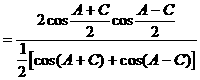

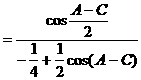
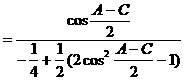
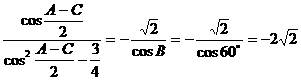
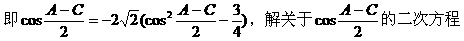
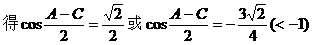

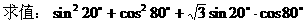

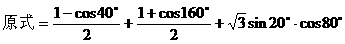
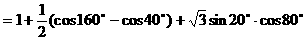
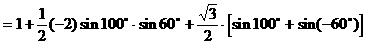
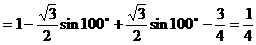
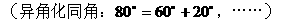
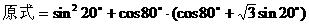
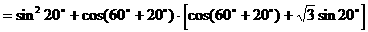
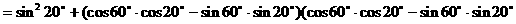

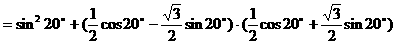
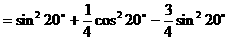
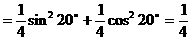
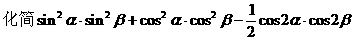
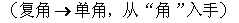
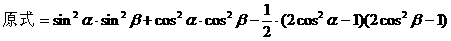
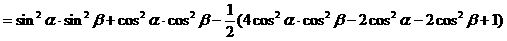
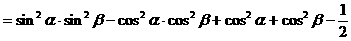
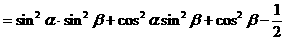
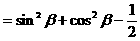
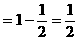
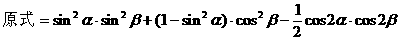
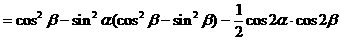
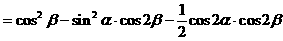
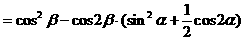
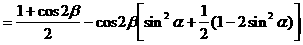
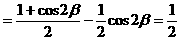
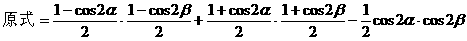
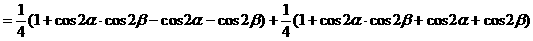
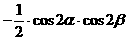
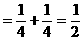
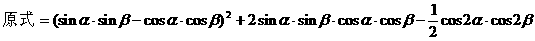

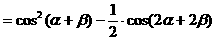
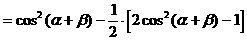
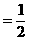
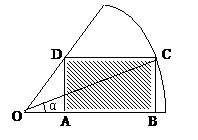
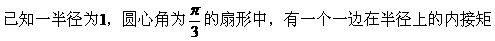 形ABCD,(如图),求该矩形的最大面积。
形ABCD,(如图),求该矩形的最大面积。