4、方法要灵活
不要把选择题简单地等同于填空题、计算题、证明题。要充分注意用题目提供的信息,灵活运用各种解法,避繁就简,才能事半功倍。
例26、P是边长为2的正方形内切圆圆周上一点,P对正方形两对角线视角分别是 ,则
,则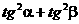 的值
( C )
的值
( C )
(A)2 (B)4 (C)8
(D)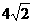
解:抓住特点用特殊值法,可迅速求解。不妨取P点为正方形对角线与它的内切圆的交点,不难求得: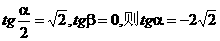 ,代入得
,代入得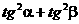 =8
=8
例27、曲线 与直线
与直线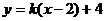 有两交点时,实数
有两交点时,实数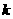 的取值范围
( A )
的取值范围
( A )
(A)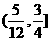 (B)
(B)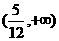 (C)
(C)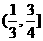 (D)
(D)
解:首先数形结合作出两函数图象,前者为圆心为(0,1)半径为2的上半圆,后者为过定点(2,4)的直线系。如图。有两交点需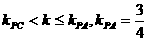 故排除(B)、(D)。那么切线
故排除(B)、(D)。那么切线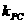 到底是
到底是 ,由选择支中反复出现的
,由选择支中反复出现的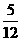 已暗示了答案可能是(A),可进一步代值,由圆心到直线的距离等于半径来验证
已暗示了答案可能是(A),可进一步代值,由圆心到直线的距离等于半径来验证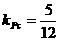 故选(A)
故选(A)
 y
P
C
A
B
O
X y
P
C
A
B
O
X |
例28、梯子10级,一步上一级或2级,规定8步走完有多少种走法 ( B )
(A)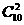 (B)
(B)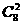 (C)
(C)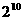 (D)
(D)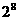
解:设2级需x步,1级y步,有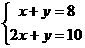 x=2,y=6即10=2
x=2,y=6即10=2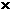 2+6
2+6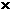 1,进一步研究2步2级的不同位置,故为
1,进一步研究2步2级的不同位置,故为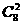 。选(B)
。选(B)
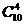 种,其中4点共面的情况有三类。一类:4点位于四面体的同一面内,有
种,其中4点共面的情况有三类。一类:4点位于四面体的同一面内,有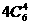 种;二类:中位线构成的平行四边形,有3种;三类:取一棱上3点及对棱的中点,有6种。(最易忽略)故取法有:
种;二类:中位线构成的平行四边形,有3种;三类:取一棱上3点及对棱的中点,有6种。(最易忽略)故取法有: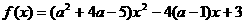 的图象在x轴上方,则实数
的图象在x轴上方,则实数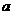 的取值范围 制 ( B )
的取值范围 制 ( B )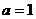 函数退缩为常函数
函数退缩为常函数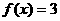 也满足条件,故选(B)
也满足条件,故选(B) (B)
(B)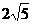 (C)
(C)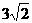 (D)
(D)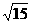
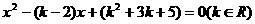 的两实根,则
的两实根,则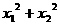 最大值是
( B )
最大值是
( B )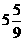 (D)不存在
(D)不存在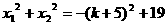 若忽略两实根
若忽略两实根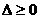 的约束,易错选(A)
的约束,易错选(A)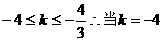 时,最大值为18
时,最大值为18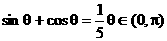 求
求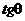 的值
( C )
的值
( C )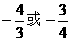 (B)
(B)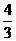 (C)
(C)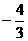 (D)
(D)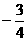
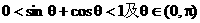 ,可判断
,可判断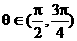 ,从而判定
,从而判定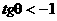 ,可直接选出(C),避免了产生增根错选(A)
,可直接选出(C),避免了产生增根错选(A)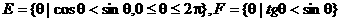 ,那么
,那么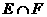 为区间
( A )
为区间
( A )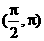 (B)
(B)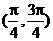 (C)
(C) (D)
(D)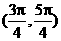
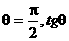 无意义,排除(B),在(D)中取
无意义,排除(B),在(D)中取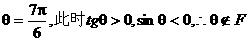 排除(D)同时也排除(C) 故选(A)
排除(D)同时也排除(C) 故选(A)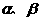 ,使得
,使得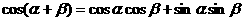
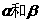 ,使得cos(
,使得cos( )=
)=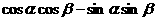
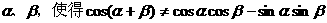
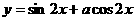 的图象关于直线
的图象关于直线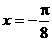 对称,那么
( D )
对称,那么
( D )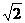 (B)-
(B)-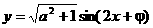 不知如何下手。应注意其对称轴过图象波峰波谷,即最值处。将
不知如何下手。应注意其对称轴过图象波峰波谷,即最值处。将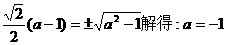 。采用将各值代入验证排除更易推出选(D)
。采用将各值代入验证排除更易推出选(D)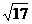 ,|a-n|=4,则向量a为 ( )
A、(-3,±4) B、(4,
±3)
C、(3, ±4) D、(-4,
±3)
,|a-n|=4,则向量a为 ( )
A、(-3,±4) B、(4,
±3)
C、(3, ±4) D、(-4,
±3)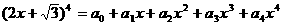 ,则
,则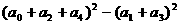 的值为()
的值为()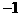 C. 0 D. 2
C. 0 D. 2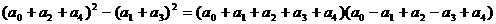
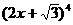 结构中,取特殊值
结构中,取特殊值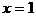 与
与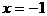 时的积.
时的积.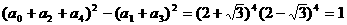 ,故选A
,故选A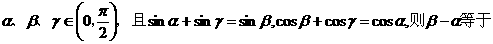
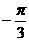 B、
B、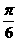 C、
C、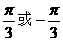 D、
D、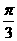 ( )
( )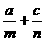 的值为
( )
的值为
( )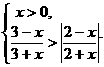 的解集是
( C )
的解集是
( C )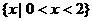 (B)
(B)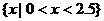
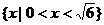 (D)
(D)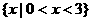
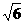 、2.5、3四个数值非常接近。让学生不易取值排除。但聪明的发现将x=
、2.5、3四个数值非常接近。让学生不易取值排除。但聪明的发现将x=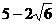 ,考虑不等式解与方程有关,猜答案为(C)
,考虑不等式解与方程有关,猜答案为(C)