0 445816 445824 445830 445834 445840 445842 445846 445852 445854 445860 445866 445870 445872 445876 445882 445884 445890 445894 445896 445900 445902 445906 445908 445910 445911 445912 445914 445915 445916 445918 445920 445924 445926 445930 445932 445936 445942 445944 445950 445954 445956 445960 445966 445972 445974 445980 445984 445986 445992 445996 446002 446010 447348
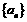 的前
的前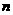 项和为
项和为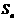 ,公差
,公差 . 若存在正整数
. 若存在正整数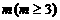 ,使得
,使得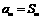 ,则当
,则当 (
( )时,有
)时,有 (填“>”、“<”、“=”).
(填“>”、“<”、“=”). 
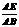 =m,
=m,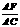 =n,则
=n,则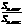 = mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
= mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若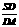 = m,
= m,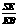 =n,
=n, = p,则
= p,则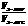 =
= 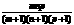
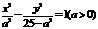 的左右两焦点分别为
的左右两焦点分别为 ,
,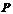 是双曲线右支上的一点,
是双曲线右支上的一点,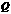 点满足
点满足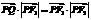 ,
,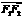 在
在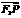 上的投影的大小恰为
上的投影的大小恰为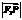 ,且它们的夹角为
,且它们的夹角为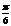 ,则
,则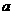 等于
等于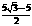 B.
B.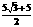 C.
C.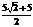 D.
D.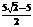
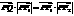 ,所以
,所以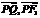 是一对同向向量,且
是一对同向向量,且 .
.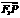 上的投影的大小恰为
上的投影的大小恰为 ,所以
,所以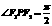 .
.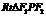 中,
中, 又
又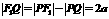 ,
,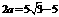 ,所以
,所以 ,故选A.
,故选A.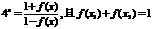 ,则
,则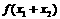 的最小值为( B )
的最小值为( B )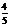 C.2 D.
C.2 D.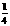
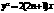 ,过
,过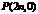 任作直线
任作直线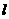 交抛物线于
交抛物线于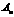 ,
,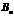 两点,则数列
两点,则数列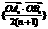 的前
的前 ,
,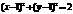 ,则两圆的公切线方程为(A)
,则两圆的公切线方程为(A) B、
B、 C、
C、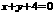 D、
D、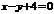
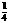 B.
B.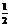 C.1
D.2
C.1
D.2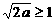 ,则M(a)=a,若
,则M(a)=a,若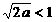 ,则M(a)=f(1)=1-a,从而M(a)=
,则M(a)=f(1)=1-a,从而M(a)=
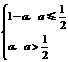 ,
M(a)min=
,
M(a)min=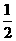 .
. 的值等于 ( C )A.25 B.24 C.-25 D.-24
的值等于 ( C )A.25 B.24 C.-25 D.-24