0 445573 445581 445587 445591 445597 445599 445603 445609 445611 445617 445623 445627 445629 445633 445639 445641 445647 445651 445653 445657 445659 445663 445665 445667 445668 445669 445671 445672 445673 445675 445677 445681 445683 445687 445689 445693 445699 445701 445707 445711 445713 445717 445723 445729 445731 445737 445741 445743 445749 445753 445759 445767 447348
 展开式的第5项等于
展开式的第5项等于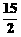 ,则x的值是
,则x的值是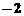 (C)
(C)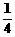 (D)
(D)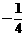
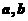 ,平面
,平面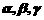 ,则使
,则使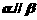 成立的一个充分条件是
成立的一个充分条件是 (B)
(B)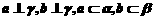
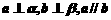 (D)
(D)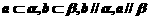
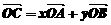 ,则
,则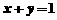 (B)
(B)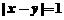 (C)
(C)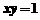 (D)
(D)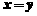
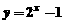 的图像是
的图像是
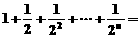
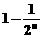 (B)
(B)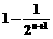 (C)
(C)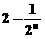 (D)
(D)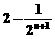
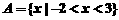 ,
, ,则
,则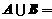
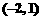 (B)
(B)
 (D)
(D)
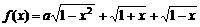 的最大值为g(a)。
的最大值为g(a)。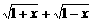 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)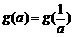 的所有实数a
的所有实数a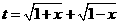
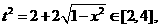 t≥0
①
t≥0
①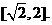 由①得
由①得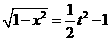
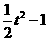 )+t=
)+t=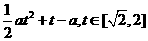
 的最大值。
的最大值。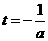 是抛物线
是抛物线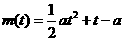 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。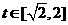 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,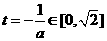 ,即
,即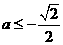 则
则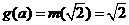
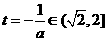 ,即
,即 则
则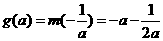
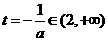 ,即
,即 则
则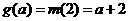
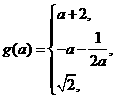
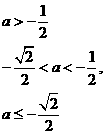
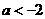 时
时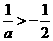 ,此时
,此时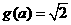 ,
,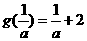
 ,与a<-2矛盾。
,与a<-2矛盾。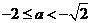
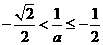 时,此时
时,此时
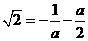 解得,
解得, 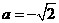 与
与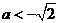 矛盾。
矛盾。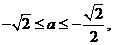
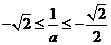 时,此时
时,此时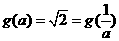
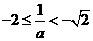 ,此时
,此时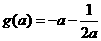 ,
,
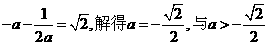 矛盾。
矛盾。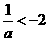 ,此时g(a)=a+2,
,此时g(a)=a+2,
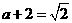 解得
解得 矛盾。
矛盾。 ,此时g(a)=a+2,
,此时g(a)=a+2, 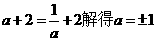 ,由a>0得a=1.
,由a>0得a=1.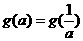 的所有实数a为
的所有实数a为 + x
+ x |(x
|(x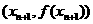 处的切线与经过(0,0)和(x
处的切线与经过(0,0)和(x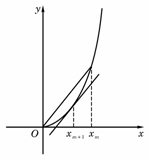 .
.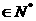 时,
时,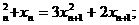
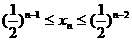
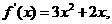
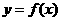 在
在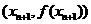 处的切线斜率
处的切线斜率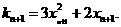
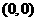 和
和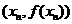 两点的直线斜率是
两点的直线斜率是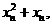
 .
.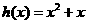 当
当 时单调递增,
时单调递增,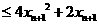
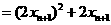 ,
,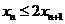 ,即
,即