19.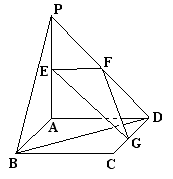 (本题满分14分)如图,平面
(本题满分14分)如图,平面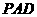 ⊥平面
⊥平面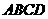 ,
,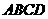 为正方形,
为正方形,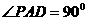 ,且
,且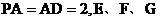 分别是线段
分别是线段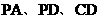 的中点。
的中点。
(1)求证: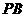 //平面
//平面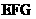 ; (2)求异面直线
; (2)求异面直线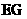 与
与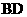 所成的角;
所成的角;
|
 上是否存在一点
上是否存在一点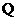 ,使得点
,使得点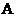 到平面
到平面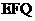 的距离为
的距离为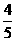 .若存在,求出
.若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
19. (本题满分14分)如图,平面
(本题满分14分)如图,平面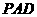 ⊥平面
⊥平面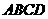 ,
,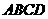 为正方形,
为正方形,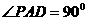 ,且
,且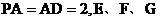 分别是线段
分别是线段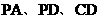 的中点。
的中点。
(1)求证: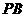 //平面
//平面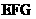 ; (2)求异面直线
; (2)求异面直线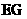 与
与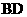 所成的角;
所成的角;
|
 上是否存在一点
上是否存在一点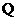 ,使得点
,使得点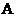 到平面
到平面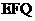 的距离为
的距离为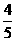 .若存在,求出
.若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。