0 445529 445537 445543 445547 445553 445555 445559 445565 445567 445573 445579 445583 445585 445589 445595 445597 445603 445607 445609 445613 445615 445619 445621 445623 445624 445625 445627 445628 445629 445631 445633 445637 445639 445643 445645 445649 445655 445657 445663 445667 445669 445673 445679 445685 445687 445693 445697 445699 445705 445709 445715 445723 447348
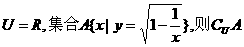 = ( )
= ( )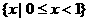 B.
B.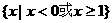
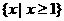 D.
D.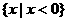
 的图像与直线
的图像与直线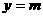 相切,并且切点的横坐标依次成公差为
相切,并且切点的横坐标依次成公差为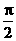 的等差数列.
的等差数列.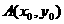 是
是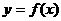 图像的对称中心,且
图像的对称中心,且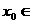 [0,
[0,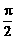 ],求点A的坐标.
],求点A的坐标.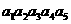 ,其中A的各数位中,
,其中A的各数位中,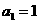 ,
,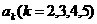 出现0概率为
出现0概率为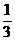 ,出现1的概率为
,出现1的概率为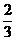 ,例如A=10011,其中
,例如A=10011,其中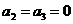 ,
, ,设
,设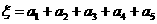 ,当启动仪器一次时,求:
,当启动仪器一次时,求: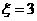 的概率。
的概率。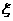 的数学期望。
的数学期望。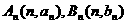
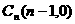 ,满足向量
,满足向量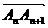 与向量
与向量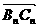 共线,且点(n,
Bn)在方向向量为(1,6)的直线上,
共线,且点(n,
Bn)在方向向量为(1,6)的直线上,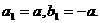
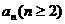 ;
;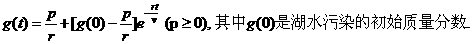 。
。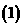 当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
当湖水污染质量分数为常数时,求湖水污染的初始质量分数;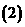 求证:当
求证:当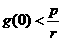 时,湖泊的污染程度越来越严重。
时,湖泊的污染程度越来越严重。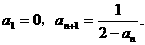
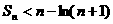 ;
;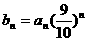 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有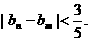
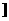 上的最大值为-3,求a的值;
上的最大值为-3,求a的值;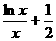 是否有实数解.
是否有实数解.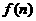 为
为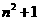
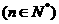 的各位数字之和,如
的各位数字之和,如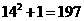 ,
,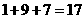 ,则
,则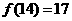 ;记
;记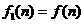 ,
,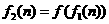 ,…,
,…,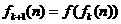 ,
,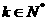 ,则
,则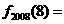 。
。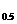 (x2+2x+a)的值域为R,命题q:函数y=-(5-2a)x是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是___________.
(x2+2x+a)的值域为R,命题q:函数y=-(5-2a)x是减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是___________.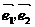 是两个互相垂直的单位向量,
是两个互相垂直的单位向量,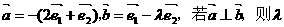 的值为
。
的值为
。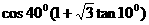 的值等于
。
的值等于
。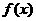 的定义域为
的定义域为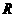 ,若存在与
,若存在与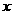 无关的正常数
无关的正常数 使
使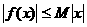 对一切实数
对一切实数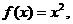 ②
②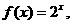 ③
③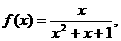 ④
④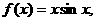 其中是“有界泛函”的个数为
其中是“有界泛函”的个数为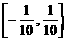 B、
B、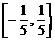 C、
C、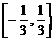 D、
D、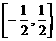
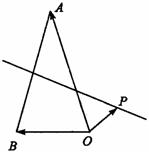
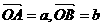 ,且P在线段AB的垂直平分线上,向量
,且P在线段AB的垂直平分线上,向量 。若|a|=3,|b|=2,则c·(a-b)的值为
。若|a|=3,|b|=2,则c·(a-b)的值为
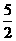 D、
D、