15、在圆 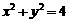 上,与直线4x+3y-12=0的距离最小的点的坐标
.
上,与直线4x+3y-12=0的距离最小的点的坐标
.
|
题次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
|
|
|
|
|
|
|
|
|
|
15、在圆 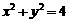 上,与直线4x+3y-12=0的距离最小的点的坐标
.
上,与直线4x+3y-12=0的距离最小的点的坐标
.
|
题次 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
|
|
|
|
|
|
|
|
|
|