0 43481 43489 43495 43499 43505 43507 43511 43517 43519 43525 43531 43535 43537 43541 43547 43549 43555 43559 43561 43565 43567 43571 43573 43575 43576 43577 43579 43580 43581 43583 43585 43589 43591 43595 43597 43601 43607 43609 43615 43619 43621 43625 43631 43637 43639 43645 43649 43651 43657 43661 43667 43675 447348




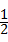 BC=8,
BC=8, =
= =6,
=6,



 cm
cm D、
D、


 AB∥CD,
AB∥CD, 在同一直角坐标系中的图象大致是( )
在同一直角坐标系中的图象大致是( ) B、
B、
 D、
D、
 中自变量x的取值范围是( )
中自变量x的取值范围是( ) =
=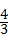 ,
,