0 43483 43491 43497 43501 43507 43509 43513 43519 43521 43527 43533 43537 43539 43543 43549 43551 43557 43561 43563 43567 43569 43573 43575 43577 43578 43579 43581 43582 43583 43585 43587 43591 43593 43597 43599 43603 43609 43611 43617 43621 43623 43627 43633 43639 43641 43647 43651 43653 43659 43663 43669 43677 447348
 如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( ) B.
B.  C.
C.  D.
D.
 可以看作是由抛物线
可以看作是由抛物线 按下列何种变换得到( )
按下列何种变换得到( ) A. 向上平移5个单位 B. 向下平移5个单位 C. 向左平移5个单位 D. 向右平移5个单位
A. 向上平移5个单位 B. 向下平移5个单位 C. 向左平移5个单位 D. 向右平移5个单位 )在平面直角坐标系的第一象限内,则a的取值范围在数轴上可表示为( )
)在平面直角坐标系的第一象限内,则a的取值范围在数轴上可表示为( )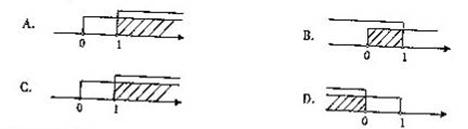
 B.
B.  C.
C.  D.
D.
 的相反数是( )
的相反数是( )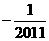 C. 2011 D.
C. 2011 D. 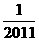
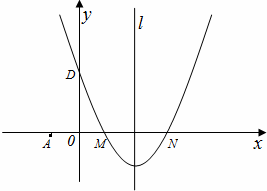
 ,即可求出圆的半径,即可得出P点的坐标.
,即可求出圆的半径,即可得出P点的坐标.
 AC×BC=6,
AC×BC=6, ,
, ,
, x+
x+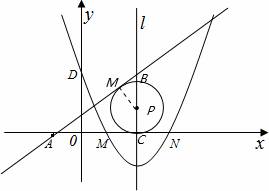 MO⊥AB,AM=AC,PM=PC,
MO⊥AB,AM=AC,PM=PC, ,
,