0 43473 43481 43487 43491 43497 43499 43503 43509 43511 43517 43523 43527 43529 43533 43539 43541 43547 43551 43553 43557 43559 43563 43565 43567 43568 43569 43571 43572 43573 43575 43577 43581 43583 43587 43589 43593 43599 43601 43607 43611 43613 43617 43623 43629 43631 43637 43641 43643 43649 43653 43659 43667 447348
 ,
,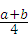
 .
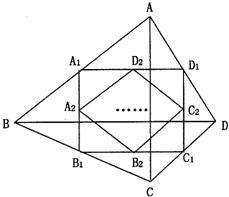
.
 A3B3=
A3B3=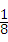 (a+b)=
(a+b)=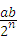 ;
;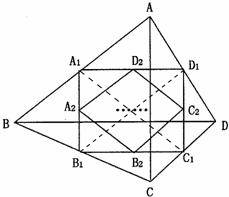
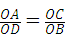 ,又由对顶角相等,即可根据对应边成比例且夹角相等的三角形相似证得相似.
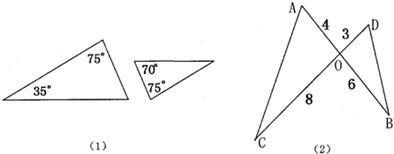
,又由对顶角相等,即可根据对应边成比例且夹角相等的三角形相似证得相似.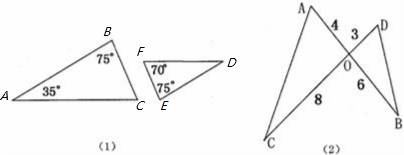 如图(1)∵∠A=35°,∠B=75°,
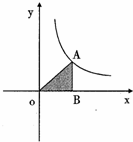
如图(1)∵∠A=35°,∠B=75°,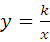 的图象上的一点,AB丄x轴于点B,且△ABO的面积是3,则k的值是( )
的图象上的一点,AB丄x轴于点B,且△ABO的面积是3,则k的值是( )