摘要:如图.四边形ABCD中.AC=a.BD=b.且AC丄BD.顺次连接四边形ABCD 各边中点.得到四边形A1B1C1D1.再顺次连接四边形A1B1C1D1各边中点.得到四边形A2B2C2D2-.如此进行下去.得到四边形AnBnCnDn.下列结论正确的有( ) ①四边形A2B2C2D2是矩形, ②四边形A4B4C4D4是菱形, ③四边形A5B5C5D5的周长是 ④四边形AnBnCnDn的面积是. A.①② B.②③ C.②③④ D.①②③④ 考点:三角形中位线定理,菱形的判定与性质,矩形的判定与性质. 专题:规律型. 分析:首先根据题意.找出变化后的四边形的边长与四边形ABCD中各边长的长度关系规律.然后对以下选项作出分析与判断: ①根据矩形的判定与性质作出判断, ②根据菱形的判定与性质作出判断, ③由四边形的周长公式:周长=边长之和.来计算四边形A5B5C5D5的周长, ④根据四边形AnBnCnDn的面积与四边形ABCD的面积间的数量关系来求其面积. 解答:解:①连接A1C1.B1D1. ∵在四边形ABCD中.顺次连接四边形ABCD 各边中点.得到四边形A1B1C1D1. ∴A1D1∥BD.B1C1∥BD.C1D1∥AC.A1B1∥AC, ∴A1D1∥B1C1.A1B1∥C1D1. ∴四边形ABCD是平行四边形, ∴B1D1=A1C1(平行四边形的两条对角线相等), ∴A2D2=C2D2=C2B2=B2A2. ∴四边形A2B2C2D2是菱形, 故本选项错误, ②由①知.四边形A2B2C2D2是菱形, ∴根据中位线定理知.四边形A4B4C4D4是菱形, 故本选项正确, ③根据中位线的性质易知.A5B5=A3B3=×A1B1=××AB.B5C5=B3C3=×B1C1=××BC. ∴四边形A5B5C5D5的周长是2×(a+b)=, 故本选项正确, ④∵四边形ABCD中.AC=a.BD=b.且AC丄BD. ∴S四边形ABCD=ab, 由三角形的中位线的性质可以推知.每得到一次四边形.它的面积变为原来的一半. 四边形AnBnCnDn的面积是, 故本选项错误, 综上所述.②③④正确, 故选C. 点评:本题主要考查了菱形的判定与性质.矩形的判定与性质及三角形的中位线定理(三角形的中位线平行于第三边且等于第三边的一半).解答此题时.需理清菱形.矩形与平行四边形的关系.
网址:http://m.1010jiajiao.com/timu3_id_435707[举报]
 26、如图,四边形ABCD中,AD∥BC,且AD=4,三角形ABC的周长为14,将三角形ABC平移到三角形DEF的位置.
26、如图,四边形ABCD中,AD∥BC,且AD=4,三角形ABC的周长为14,将三角形ABC平移到三角形DEF的位置. 如图在四边形ABCD中,∠1和∠2分别是∠A和∠C的外角,且∠B+∠D=140°,则∠1+∠2=
如图在四边形ABCD中,∠1和∠2分别是∠A和∠C的外角,且∠B+∠D=140°,则∠1+∠2= (2012•南充)如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积为24cm2,则AC长是
(2012•南充)如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积为24cm2,则AC长是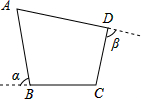 如图:四边形ABCD中,∠α、∠β分别是∠B、∠D的
如图:四边形ABCD中,∠α、∠β分别是∠B、∠D的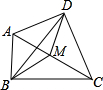 已知,如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC的中点.求证:MD=MB.
已知,如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC的中点.求证:MD=MB.