22.如图,这些等腰三角形与正三角形的形状有差异,我们把这与正三角形的接近程度称为“正度”。在研究“正度”时,应保证相似三角形的“正度”相等。
|

 设等腰三角形的底和腰分别为a、b,底角和顶角分别为α,β。要求“正度”的值是非负数。
设等腰三角形的底和腰分别为a、b,底角和顶角分别为α,β。要求“正度”的值是非负数。
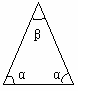
同学甲认为:可用式子|a-b|来表示“正度”,|a-b|的值越小,表示等腰三角形越接近正三角形;
同学乙认为:可用式子|α-β|来表示“正度”,|α-β|的值越小,表示等腰三角形越接近正三角形;
探究:⑴他们的方案哪个较合理,为什么?
⑵对你认为不够合理的方案,请加以改进(给出式子即可);
⑶请再给出一种衡量“正度”的表达式。
20.某旅行社组团去外地旅游,20人一起组团,每人单价为1200元。如果每团超过20人时,给予优惠,每增加一人,单价减少20元。
⑴设旅行社每团营业额为y元,人数为x人。则每团人数为多少时,旅行社可获得最大营业额?
⑵若该旅行社组团费用Q=6x2+18000,那么为获得最大利润,每团有多少人最适宜。

|
 ⑴若点E在BC上运动(E与B、C不重合),点F在CA上
⑴若点E在BC上运动(E与B、C不重合),点F在CA上
运动,且EF平分△ABC的周长,设CE=x,△CEF的面积
为
|
|
1)x=3时,求y的值
2)求y与x之间的函数关系式,并写出自变量的取值
|
3)以E为圆心,EC为半径作一个圆。试问:当x为何值时,此圆与AB相切
18.某商场用5万元购进一批儿童玩具,加价30%销售,很快脱销,商场决定再进一批。因材料涨价,所以该玩具比进货价每件贵2元。第二次用10.8万元购进第一批数量的2倍,当商场卖到一半时发现该玩具销量收益下降。所以决定以原价的八五折售出,很快售完。
⑴问2次共购进多少间玩具?
⑵商场卖这种玩具共盈利多少元?
|
|
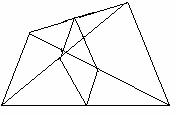 ⑴四边形EFGH是什么四边形?请证明。
⑴四边形EFGH是什么四边形?请证明。
|
|
|
⑵四边形ABCD有什么条件时,四边形EFGH是菱形?
|
|
||||
|
|||||
⑶四边形EFGH可能是正方形吗?
17.⑴某校课外数学小组要测量校园内的旗杆,现有米尺一把,不可以爬上旗杆,你可以再选一件或工件工具(也可不选)设计一个测量方案,并画出草图。
|
|
|
|


 ⑵小明、小亮是一个活动小组,他们没有选用其它工具,而是这样做的,小明站在杆影下,让头顶的影子恰好与杆顶的影子重合。小亮测得旗杆到小明的距离为5.7米,小明到影子顶端的水平距离为2.3米,请你帮他们求求旗杆的高度。(精确到0.1米)
⑵小明、小亮是一个活动小组,他们没有选用其它工具,而是这样做的,小明站在杆影下,让头顶的影子恰好与杆顶的影子重合。小亮测得旗杆到小明的距离为5.7米,小明到影子顶端的水平距离为2.3米,请你帮他们求求旗杆的高度。(精确到0.1米)
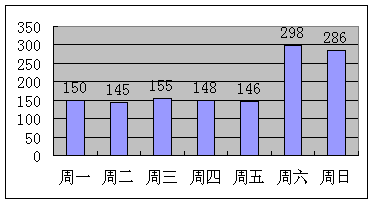
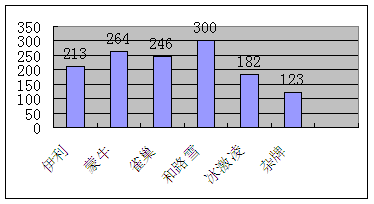
15.小红的奶奶在公园里卖冷饮,小红对奶奶一星期每天卖冰糕的数量、品种进行统计如下。
|
|
⑴求出一周七天卖冰糕的中位数、平均数。
⑵每天卖冰糕的平均数,能否反映真实水平?请说明理由。
⑶请为奶奶的进货提出合理化的建议:
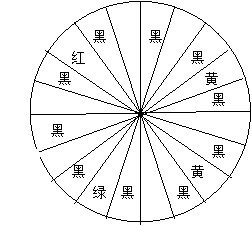 小明和小亮一天在广场上玩,看见有人在设摊“摸彩”。
小明和小亮一天在广场上玩,看见有人在设摊“摸彩”。
 (2)A、B、C是三个放牧点,要修建一个牧民定居点,使三个放牧点到定居点的距离相等。
(2)A、B、C是三个放牧点,要修建一个牧民定居点,使三个放牧点到定居点的距离相等。