椭圆的基本概念
〖考试内容〗椭圆及其标准方程,焦点、焦距,范围、对称性、顶点、长轴、短轴、离心率、准线,椭圆的画法.
〖考试要求〗掌握椭圆标准方程及几何性质,会根据所给条件画出椭圆,了解椭圆的一些实际应用.
〖双基回顾〗
定义
1
到两个定点的距离之和等于定值的点的轨迹
2
 到定点的距离与到定直线的距离之比等于定值(小于1)的点的轨迹
到定点的距离与到定直线的距离之比等于定值(小于1)的点的轨迹
图形

顶点
焦点
长轴
短轴
焦距
准线方程
离心率
焦半径
〖知识点训练〗
1、平面上P点到定点F1、F2距离之和等于|F1F2|,则P点的轨迹是………………………………( )
(A)椭圆 (B)直线F1F2 (C)线段F1F2 (D) F1F2中垂线
2、若椭圆经过原点,且焦点为 ,则其离心率为………………………………( )
,则其离心率为………………………………( )
(A) (B)
(B) (C)
(C) (D)
(D)
3、椭圆 的一个焦点是(0,2),那么k等于……………………………………( )
的一个焦点是(0,2),那么k等于……………………………………( )
(A)-1 (B)1 (C) (D)-
(D)-
〖例题分析〗
1、已知椭圆的焦点为F1(0,-1)、F2(0,1),直线y=4是其一条准线.
⑴求此椭圆方程;
⑵又设P在椭圆上并且满足|PF1|-|PF2|=1,求tg∠F1PF2.
2、F1、F2是椭圆 焦点,AB是经过F1的弦,如果|AB|=8,求△AF2B的周长。
焦点,AB是经过F1的弦,如果|AB|=8,求△AF2B的周长。
 3、已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O是AB中点,点E、F、G分别在BC、CD、DA上移动,并且
3、已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O是AB中点,点E、F、G分别在BC、CD、DA上移动,并且 ,P是GE、OF交点,问是否存在两个定点,使P到这两个定点的距离和为定值?如果存在,求出这两个点的坐标及此定值,如果不存在,说明理由!(2003广东高考题)
,P是GE、OF交点,问是否存在两个定点,使P到这两个定点的距离和为定值?如果存在,求出这两个点的坐标及此定值,如果不存在,说明理由!(2003广东高考题)
〖课堂练习〗
 1、椭圆
1、椭圆 的离心率为
的离心率为 ,则实数m= .
,则实数m= .
2、如图,F是椭圆焦点,A是顶点,l是准线,则在下列关系:e = ,e =
,e = ,e =
,e = ,e =
,e = ,e =
,e = 中,能正确表示离心率的有( )(A)2个
(B)3个 (C)4个 (D) 5个
中,能正确表示离心率的有( )(A)2个
(B)3个 (C)4个 (D) 5个
〖能力测试〗 姓名 得分
1、椭圆 的准线平行于x轴,则有…………………………………………( )
的准线平行于x轴,则有…………………………………………( )
(A)0<m< (B)m<
(B)m< 且m≠0 (C)m>0且m≠1 (D)
m>
且m≠0 (C)m>0且m≠1 (D)
m> 且m≠1
且m≠1
2、如果椭圆的两个顶点为(3,0),(0,4),则其标准方程为………………………………( )
(A) (B)
(B) (C)
(C) (D)
(D)
3、椭圆的两个焦点和中心把准线间的距离四等份,则其焦点对短轴端点张角为……………( )
(A)45º (B)60º (C)90º (D) 120º
4、F1、F2是椭圆 焦点,点P在椭圆上线段PF1的中点在y轴上,则|PF1|是|PF2|的( )
焦点,点P在椭圆上线段PF1的中点在y轴上,则|PF1|是|PF2|的( )
(A)7倍 (B)5倍 (C)4倍 (D)3倍
5、椭圆 上有一点P(P在第一象限内)满足PF1⊥PF2,则点P坐标为
.
上有一点P(P在第一象限内)满足PF1⊥PF2,则点P坐标为
.
6、求以椭圆 的长轴端点为短轴端点,并且经过点P(-4,1)的椭圆方程.
的长轴端点为短轴端点,并且经过点P(-4,1)的椭圆方程.
 7、点M是椭圆
7、点M是椭圆 上的一点,F1、F2是左右焦点,∠F1MF2=60º,求△F1MF2的面积.
上的一点,F1、F2是左右焦点,∠F1MF2=60º,求△F1MF2的面积.
直线与椭圆的位置关系
〖考试内容〗椭圆及其标准方程,焦点、焦距,范围、对称性、顶点、长轴、短轴、离心率、准线,椭圆的画法.
〖复习要求〗掌握直线与椭圆位置关系的判定方法――“△”法;
掌握弦长公式 ;“韦达定理、设而不求”的技巧在解题中的使用.
;“韦达定理、设而不求”的技巧在解题中的使用.
〖知识点训练〗
1、直线x=2与椭圆 的交点个数为…………………………………………………( )
的交点个数为…………………………………………………( )
(A)0个 (B)1个 (C) 2个 (D) 3个
2、直线y=1被椭圆 截得的线段长为………………………………………………( )
截得的线段长为………………………………………………( )
(A)4 (B)3
(B)3 (C) 2
(C) 2 (D)
(D) 
3、直线y=mx+1与椭圆x2+4y2=1有且只有一个交点,则m2=………………………………( )
(A) (B)
(B) (C)
(C)  (D)
(D) 
4、椭圆 的长轴端点为M、N,不同于M、N的点P在此椭圆上,那么PM、PN的斜率之积为…………………………………………………………………………………………( )
的长轴端点为M、N,不同于M、N的点P在此椭圆上,那么PM、PN的斜率之积为…………………………………………………………………………………………( )
(A)- (B)-
(B)- (C)
(C)  (D)
(D) 
〖例题分析〗
1、椭圆 的焦点为
的焦点为 点P为其上的动点,当
点P为其上的动点,当 为钝角时,求点P的横坐标的取值范围.
为钝角时,求点P的横坐标的取值范围.
2、已知椭圆C的焦点分别为 ,长轴长为6,设直线
,长轴长为6,设直线 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。
3、椭圆E: 内有一点P(2,1),求经过P并且以P为中点的弦所在直线方程.
内有一点P(2,1),求经过P并且以P为中点的弦所在直线方程.
4、过P(- ,0)作一直线l交椭圆E:11x2+y2=9于M、N两点,问l的倾斜角多大时,以M、N为直径的圆过原点?
,0)作一直线l交椭圆E:11x2+y2=9于M、N两点,问l的倾斜角多大时,以M、N为直径的圆过原点?
〖课堂练习〗
如果焦点是F(0,±5 )的椭圆截直线3x-y-2=0所得弦的中点横坐标为
)的椭圆截直线3x-y-2=0所得弦的中点横坐标为 ,求此椭圆方程.
,求此椭圆方程.
〖课堂小结〗
解决直线与椭圆位置关系问题时,对于消元后的一元二次方程必须讨论二次项系数和“△”;另外,韦达定理和设而不求的技巧是必须掌握的.
〖能力测试〗 姓名 得分
1、已知点(4,2)是直线l被椭圆 所截得的弦中点,则l方程是………………( )
所截得的弦中点,则l方程是………………( )
(A)x-2y=0 (B)x+2y-4=0 (C)2x+3y+4=0 (D) x+2y-8=0
2、椭圆 上有三点A(x1,y1)、B(4,
上有三点A(x1,y1)、B(4, )、C(x2,y2),如果A、B、C三点到焦点F(4,0)的距离成等差数列,则x1+x2=
.(提示:利用焦半径公式)
)、C(x2,y2),如果A、B、C三点到焦点F(4,0)的距离成等差数列,则x1+x2=
.(提示:利用焦半径公式)
3、直线x-y+1=0被椭圆 截得的弦长为
.
截得的弦长为
.
4、椭圆E:ax2+by2=1与直线x+y=1交于A、B两点,M是AB中点,如果|AB|=2 ,且OM的斜率为
,且OM的斜率为 . (1)把M点的坐标用a、b表示出来; (2)求此椭圆方程.
. (1)把M点的坐标用a、b表示出来; (2)求此椭圆方程.
双曲线(1)
〖考试内容〗双曲线及其标准方程,焦点、焦距,范围、对称性、顶点、长轴、短轴、离心率、准线,双曲线的画法.
〖考试要求〗掌握双曲线标准方程及几何性质,了解双曲线的一些实际应用.
定义
1
到两个定点的距离之和等于定值的点的轨迹
2
到定点的距离与到定直线的距离之比等于定值(小于1)的点的轨迹
图形


标准方程
顶点
焦点
焦距
准线方程
离心率
焦半径
渐近线
〖双基回顾〗
〖知识点训练〗
1、焦点为 经过点
经过点 的双曲线的标准方程是
.
的双曲线的标准方程是
.
2、焦点在y轴上,焦距是16,离心率为 的双曲线的标准方程是
.
的双曲线的标准方程是
.
3、方程 表示双曲线,则实数k的取值范围是……………………………………( )
表示双曲线,则实数k的取值范围是……………………………………( )
(A)(-2,-3) (B)(-∞,-2) (C) (3,+∞) (D) (-∞,-2)∪(3,+∞)
4、双曲线 的实轴长为
;离心率是 ;渐近线方程是
;准线方程是
;共轭双曲线方程是
;
的实轴长为
;离心率是 ;渐近线方程是
;准线方程是
;共轭双曲线方程是
;
〖例题分析〗
1、⑴求与双曲线 共焦点并且一条准线方程为x=-
共焦点并且一条准线方程为x=- 的双曲线方程.
的双曲线方程.
⑵求与双曲线 共渐近线,并且经过点P(2,-2)的双曲线方程.
共渐近线,并且经过点P(2,-2)的双曲线方程.
3、已知点 和
和 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线 交于D、E两点,求线段DE的长。(2002年上海高考题)
交于D、E两点,求线段DE的长。(2002年上海高考题)
*4、点P到点M(-1,0)、N(1,0)距离之差为2m,到x、y轴距离之比为2,求实数m的取值范围.(2003高考题)
〖课堂练习〗
1、双曲线的实轴长为4,虚轴长为6,焦点在y轴上,则双曲线的标准方程是………………( )
(A) (B)
(B) (C)
(C) (D)
(D) 
2、 “ab<0”是“方程ax2+by2=c表示双曲线”的………………………………………( )条件
(A)必要不充分 (B)充分不必要 (C)充分必要 (D)既不充分又不必要
〖能力测试〗 姓名 得分
1、下列方程中,以x±2y=0为渐近线的双曲线是……………………………………………( )
(A) (B)
(B) (C)
(C) (D)
(D)
2、双曲线8kx2-ky2=8的一个焦点为(0,3),则实数k=………………………………………( )
(A)1 (B)-1 (C) (D)-
(D)-
3、双曲线两准线间距离的4倍等于焦距,则离心率等于………………………………………( )
(A)1 (B)2 (C)3 (D)4
4、等轴双曲线的一个焦点为(0,-4),则其准线方程为 .
5、椭圆 与双曲线
与双曲线 有相同的焦点,则实数a=
.
有相同的焦点,则实数a=
.
6、双曲线 的离心率
的离心率 ,则实数k的取值范围是
.
,则实数k的取值范围是
.
7、若双曲线 的渐近线方程为
的渐近线方程为 ,
,
⑴求实数m之值; ⑵写出此双曲线的焦点坐标
直线与双曲线的位置关系
〖考试内容〗双曲线及其标准方程,焦点、焦距,范围、对称性、顶点、长轴、短轴、离心率、准线,双曲线的画法.
〖考试要求〗掌握双曲线标准方程及几何性质,了解双曲线的一些实际应用.
〖知识点训练〗
1、双曲线 上一点P到左焦点距离为2,则P到右焦点距离为……………………( )
上一点P到左焦点距离为2,则P到右焦点距离为……………………( )
(A)8 (B)4 (C)11或者7 (D) 8或者4
2、双曲线 上一点P到右焦点距离为8,则P到右准线距离为…………………( )
上一点P到右焦点距离为8,则P到右准线距离为…………………( )
(A) (B)10
(C)2
(B)10
(C)2 (D)
(D)
3、双曲线 与
与 有相同的………………………………………………( )
有相同的………………………………………………( )
(A)焦点 (B)准线 (C)渐近线 (D) 离心率
4、双曲线x2-y2=16左支上一点P,F1、F2是左右焦点,则|PF1|-|PF2|= .
〖例题分析〗
1、
已知双曲线 与点
与点 ,过点P作直线l与双曲线交于A、B两点,若P为AB的中点。
,过点P作直线l与双曲线交于A、B两点,若P为AB的中点。
⑴求直线AB的方程;
⑵若 ,是否存在以
,是否存在以 为中点的弦?
为中点的弦?
2、设A、B是双曲线 上的两点,点
上的两点,点 是线段AB的中点。(2002年江苏高考题)
是线段AB的中点。(2002年江苏高考题)
⑴求直线AB的方程;
⑵如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D是否共圆,为什么?
 3、在双曲线
3、在双曲线 上支上有不同三点A(x1,y1)、B(
上支上有不同三点A(x1,y1)、B( ,6)、C(x2,y2)到焦点F(0,5)的距离成等差数列.
,6)、C(x2,y2)到焦点F(0,5)的距离成等差数列.
⑴求y1+y2之值;
⑵证明AC的垂直平分线经过一个定点T并且求出这个点T的坐标.
|
 的焦点,过
的焦点,过 作垂直于x轴的直线交双曲线于点P,且
作垂直于x轴的直线交双曲线于点P,且 。则双曲线的渐近线方程为
。(2002年上海春季高考改编)
。则双曲线的渐近线方程为
。(2002年上海春季高考改编) 与直线
与直线 的交点个数是…………………………………( )
的交点个数是…………………………………( ) 被双曲线
被双曲线 截得的弦的中点坐标是
;弦长是
。
截得的弦的中点坐标是
;弦长是
。 6、 已知F1、F2是双曲线
6、 已知F1、F2是双曲线 的两个焦点,点P在双曲线上,如果∠F1PF2=
的两个焦点,点P在双曲线上,如果∠F1PF2= ,求△F1PF2的面积.
,求△F1PF2的面积.



 ,0) (B)(0,
,0) (B)(0, ) (C) (
) (C) ( 一定不会表示……………………………………………………( )
一定不会表示……………………………………………………( ) 上的点到直线x-y-2=0的最短距离是_______________。
上的点到直线x-y-2=0的最短距离是_______________。 ),求二者的方程.
),求二者的方程.
 (A)5 (B)
(A)5 (B) (C)2 (D)
(C)2 (D)
 按向量
按向量 =(3,-2)平移得曲线C2,则曲线C2的方程是…………( ) (A)x2=
=(3,-2)平移得曲线C2,则曲线C2的方程是…………( ) (A)x2= (B)(x-6)2= -8(y+4) (C)(x-1)2=-8(y-1) (D)(x-5)2=-8(y+5)
(B)(x-6)2= -8(y+4) (C)(x-1)2=-8(y-1) (D)(x-5)2=-8(y+5)
 的准方程为……………………………………………………………………( )
的准方程为……………………………………………………………………( ) (B)y=2 (C)x=
(B)y=2 (C)x= 于坐标轴交点的抛物线方程是……………………………( )
于坐标轴交点的抛物线方程是……………………………( ) 与过焦点的直线交于A,B两点,则
与过焦点的直线交于A,B两点,则 为………………………………( )
为………………………………( ) `
` 2、抛物线C的顶点在原点,焦点F是圆x2+y2-4x=0的中心.
2、抛物线C的顶点在原点,焦点F是圆x2+y2-4x=0的中心. 是否存在一对互相垂直的直线同时都与轨迹C有公共点?证明你的结论.
是否存在一对互相垂直的直线同时都与轨迹C有公共点?证明你的结论. (D) 3
(D) 3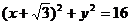 内部一点A(
内部一点A(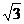 ,0)与圆周上动点Q连线AQ的中垂线交CQ于P,求点P的轨迹方程.
,0)与圆周上动点Q连线AQ的中垂线交CQ于P,求点P的轨迹方程. ,求AB的中点P的轨迹方程。
,求AB的中点P的轨迹方程。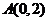 的距离减去它到x轴的距离的差都是2,求这条曲线的方程。
的距离减去它到x轴的距离的差都是2,求这条曲线的方程。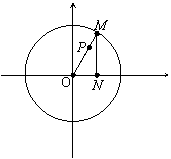
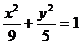 上一点,过P作其长轴垂线,M是垂足,则PM中点轨迹方程为………( )
上一点,过P作其长轴垂线,M是垂足,则PM中点轨迹方程为………( )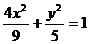 (B)
(B) 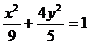 (C)
(C)  (D)
(D) 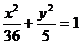
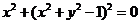 的图象是……………………………………………………………( )
的图象是……………………………………………………………( )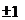 (D)以上答案均不对
(D)以上答案均不对
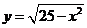
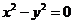
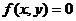 关于直线y=x+b对称曲线方程为 ;
关于直线y=x+b对称曲线方程为 ;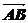 的坐标;
的坐标; 关于点A(-2,1)对称的椭圆方程为
.
关于点A(-2,1)对称的椭圆方程为
.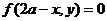 (B)
(B)  (C)
(C)  (D)
(D) 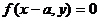
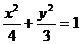 上存在两个不同的点A、B关于直线y=4x+m对称,求实数m的取值范围.
上存在两个不同的点A、B关于直线y=4x+m对称,求实数m的取值范围. 对称;
对称;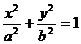 的一个焦点,直线l经过原点与此椭圆交于A、B两点,则△ABF面积最大值为…………………………………………………………………………………………( )
的一个焦点,直线l经过原点与此椭圆交于A、B两点,则△ABF面积最大值为…………………………………………………………………………………………( )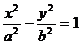 的离心率为e1、
的离心率为e1、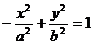 的离心率为e2,则e1+e2的最小值是( )
的离心率为e2,则e1+e2的最小值是( )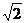 (B)2
(C)2
(B)2
(C)2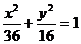 上,F是椭圆的右焦点,则|FP|max= ;|FP|min= .
上,F是椭圆的右焦点,则|FP|max= ;|FP|min= .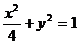 上,
上,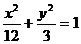 的焦点为焦点作椭圆E.
的焦点为焦点作椭圆E. ,求C的方程并且求当△AOB面积最大时的l方程.
,求C的方程并且求当△AOB面积最大时的l方程.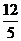 (D)
(D) 
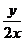 的最大值为…………………………( )
的最大值为…………………………( )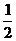 (B) -
(B) -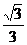 (D)
(D)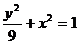 的内接矩形面积最大值为
.
的内接矩形面积最大值为
.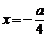 (B)
(B)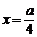 (C)
(C)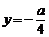
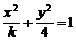 的一条准线的方程是x=5,则k 的值是………………………………( )
的一条准线的方程是x=5,则k 的值是………………………………( )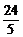 (D)
(D)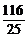
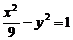 的两个焦点F1,F2,A是此双曲线上一点,且|AF1|=5,那么|AF2|=……( )
的两个焦点F1,F2,A是此双曲线上一点,且|AF1|=5,那么|AF2|=……( )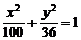 上的点P到它的左准线的距离是10,则P点到它的右焦点的距离为……( )
上的点P到它的左准线的距离是10,则P点到它的右焦点的距离为……( ) 与
与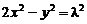 都有相同的:①焦点;②准线;③渐近线;④离心率. 以上四个结论中,正确的………………………………………………( )
都有相同的:①焦点;②准线;③渐近线;④离心率. 以上四个结论中,正确的………………………………………………( )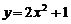 上的动点,A(0,-1),则线段PA的中点的轨迹方程是…………( )
上的动点,A(0,-1),则线段PA的中点的轨迹方程是…………( )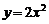 (B)
(B)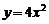 (C)
(C) (D)
(D)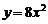
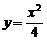 的焦点作直线交抛物线于两点
的焦点作直线交抛物线于两点 ,如果
,如果 ,那么线段AB的长为……………………………………………………………………………………( )
,那么线段AB的长为……………………………………………………………………………………( )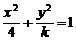 的离心率
的离心率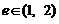 ,则k的取值范围是………………………………(
)
,则k的取值范围是………………………………(
)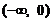 (B)
(B)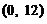 (C)
(C)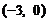 (D)
(D)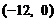
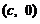 为椭圆
为椭圆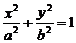 的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F的距离等于
的右焦点,F与椭圆上点的距离的最大值为M,最小值为m,则椭圆上与F的距离等于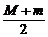 的点的坐标是…………………………………………………( )
的点的坐标是…………………………………………………( ) (B)
(B)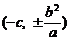 (C)
(C)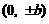 (D)
(D)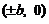
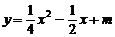 的焦点在x轴上,则m的值是………………………………( )
的焦点在x轴上,则m的值是………………………………( )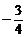 (B)
(B) (C)
(C)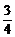 (D)
(D)
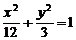 的焦点是F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的………………………………………………………………………………………( )
的焦点是F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的………………………………………………………………………………………( ) 的中心O为顶点,以其左准线为准线的抛物线与此双曲线的右准线交于A、B,则△AOB的面积等于…………………………………………………………………( )
的中心O为顶点,以其左准线为准线的抛物线与此双曲线的右准线交于A、B,则△AOB的面积等于…………………………………………………………………( )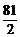 (C)
(C)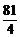 (D)
(D)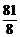
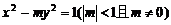 ,给出下列命题:①焦点在x轴上;②短半轴的长为1;③准线方程是
,给出下列命题:①焦点在x轴上;②短半轴的长为1;③准线方程是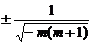 ;④离心率
;④离心率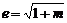 . 其中正确命题的序号是
.
. 其中正确命题的序号是
.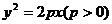 与此椭圆在第一象限交点为Q,如果
与此椭圆在第一象限交点为Q,如果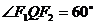 ,求:
,求: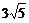 ,求此抛物线的方程.
,求此抛物线的方程.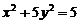 的左焦点,过点M(-1,1)引抛物线的弦使点M为弦的中点,求弦所在的直线方程,并求出弦长.
的左焦点,过点M(-1,1)引抛物线的弦使点M为弦的中点,求弦所在的直线方程,并求出弦长.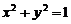 内切,与直线l:x=3相切.
内切,与直线l:x=3相切.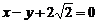
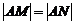 时,试求m
时,试求m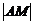 的取值范围.
的取值范围.