0 50990 50998 51004 51008 51014 51016 51020 51026 51028 51034 51040 51044 51046 51050 51056 51058 51064 51068 51070 51074 51076 51080 51082 51084 51085 51086 51088 51089 51090 51092 51094 51098 51100 51104 51106 51110 51116 51118 51124 51128 51130 51134 51140 51146 51148 51154 51158 51160 51166 51170 51176 51184 447348
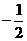 。
。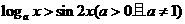 对于任意
对于任意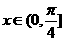 都成立,则a的取值
都成立,则a的取值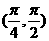 B.
B.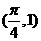 C.
C.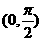 D.
D.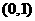
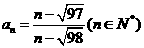 则数列的前30项中的最大值和最小值分别为 ( )
则数列的前30项中的最大值和最小值分别为 ( )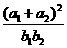 的取值范围是
( )
的取值范围是
( ) ) C.(-
) C.(-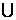 [4,+
[4,+ +
+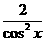 的最小值是
的最小值是
 0恒成立,则c的取值范围是
( )
0恒成立,则c的取值范围是
( ) 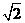 -1,+
-1,+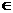 R
R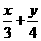 的最大值为
。
的最大值为
。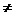 1,且bi>0(i=1,2,3,…,n)若a1=b1,a11=b11则 ( )
1,且bi>0(i=1,2,3,…,n)若a1=b1,a11=b11则 ( ) 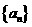 满足a1=2,an+1=an+
满足a1=2,an+1=an+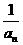 (n=1,2,3,……)
(n=1,2,3,……)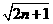 对一切正整数n成立;
对一切正整数n成立;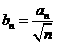 (n=1,2,3,……),判断bn与bn+1的大小。并说明理由。
(n=1,2,3,……),判断bn与bn+1的大小。并说明理由。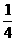 或b>
或b>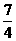 。
。 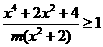 均成立,求实数m的取值范围。
均成立,求实数m的取值范围。