1、空间基本元素:直线与平面之间位置关系的小结。如下图:
|
条件 结论 |
线线平行 |
线面平行 |
面面平行 |
垂直关系 |
|
线线平行 |
如果a∥b,b∥c,那么a∥c |
如果a∥α,a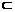 β,β∩α=b,那么a∥b β,β∩α=b,那么a∥b |
如果α∥β,α∩γ=a,β∩γ=b,那么a∥b |
如果a⊥α,b⊥α,那么a∥b |
|
线面平行 |
如果a∥b,a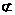 α,b α,b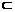 α,那么a∥α α,那么a∥α |
-- |
如果α∥β,a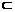 α,那么α∥β α,那么α∥β |
-- |
|
面面平行 |
如果a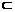 α,b α,b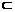 α,c α,c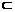 β,d β,d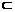 β,a∥c,b∥d,a∩b=P,那么α∥β β,a∥c,b∥d,a∩b=P,那么α∥β |
如果a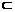 α,b α,b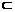 α,a∩b=P,a∥β,b∥β,那么α∥β α,a∩b=P,a∥β,b∥β,那么α∥β |
如果α∥β,β∥γ,那么α∥γ |
如果a⊥α,a⊥β,那么α∥β |
|
条件 结论 |
线线垂直 |
线面垂直 |
面面垂直 |
平行关系 |
|
线线垂直 |
二垂线定理及逆定理 |
如果a⊥α,b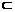 α,那么a⊥b α,那么a⊥b |
如果三个平面两两垂直,那么它们交线两两垂直 |
如果a∥b,a⊥c,那么b⊥c |
|
线面垂直 |
如果a⊥b,a⊥c,b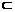 α,c α,c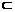 α,b∩c=P,那么a⊥α α,b∩c=P,那么a⊥α |
-- |
如果α⊥β,α∩β=b,a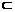 α,a⊥b,那么a⊥β α,a⊥b,那么a⊥β |
如果a⊥α,b∥a,那么b⊥α |
|
面面垂直 |
定义(二面角等于900) |
如果a⊥α,a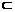 β,那么β⊥α β,那么β⊥α |
-- |
-- |
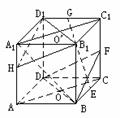 例1、在正方体ABCD-A1B1C1D1中,E、F、G、H分别为棱BC、CC1、C1D1、AA1的中点,O为AC与BD的交点(如图),求证:(1)EG∥平面BB1D1D;(2)平面BDF∥平面B1D1H;(3)A1O⊥平面BDF;(4)平面BDF⊥平面AA1C。
例1、在正方体ABCD-A1B1C1D1中,E、F、G、H分别为棱BC、CC1、C1D1、AA1的中点,O为AC与BD的交点(如图),求证:(1)EG∥平面BB1D1D;(2)平面BDF∥平面B1D1H;(3)A1O⊥平面BDF;(4)平面BDF⊥平面AA1C。 线面平行
线面平行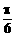 B、
B、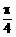 C、
C、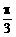 D、
D、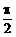
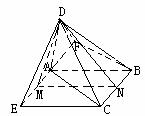 求异面直线DA与BC所成的角;
求异面直线DA与BC所成的角;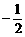 )=3a2
)=3a2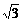 a
a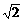 a
a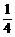
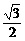 a,MN=a
a,MN=a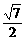 a
a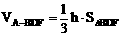 ,
,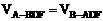
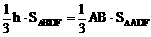
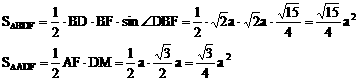
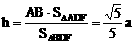 ,即异面直线BD与AC的距离为
,即异面直线BD与AC的距离为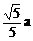
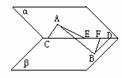 例4、如图,在600的二面角α-CD-β中,AC
例4、如图,在600的二面角α-CD-β中,AC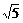 x,当x为何值时,A、B的距离最小?并求此距离。
x,当x为何值时,A、B的距离最小?并求此距离。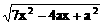 ,当x=
,当x=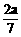 时,|AB|有最小值
时,|AB|有最小值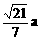 。
。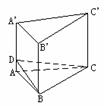 例5、如图,斜三棱柱ABC-A’B’C’中,底面是边长为a的正三角形,侧棱长为 b,侧棱AA’与底面相邻两边AB、AC都成450角,求此三棱柱的侧面积和体积。
例5、如图,斜三棱柱ABC-A’B’C’中,底面是边长为a的正三角形,侧棱长为 b,侧棱AA’与底面相邻两边AB、AC都成450角,求此三棱柱的侧面积和体积。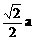
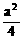
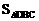 ·AA’=
·AA’=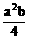
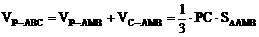
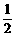 ×AB×MN=
×AB×MN=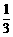 ×16×108=576(cm3)
×16×108=576(cm3)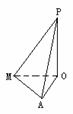 棱柱、棱锥是常见的多面体。在正棱柱中特别要运用侧面与底面垂直的性质解题,在正棱锥中,要熟记由高PO,斜高PM,侧棱PA,底面外接圆半径OA,底面内切圆半径OM,底面正多边形半边长OM,构成的三棱锥,该三棱锥四个面均为直角三角形。
棱柱、棱锥是常见的多面体。在正棱柱中特别要运用侧面与底面垂直的性质解题,在正棱锥中,要熟记由高PO,斜高PM,侧棱PA,底面外接圆半径OA,底面内切圆半径OM,底面正多边形半边长OM,构成的三棱锥,该三棱锥四个面均为直角三角形。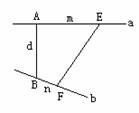 其中θ1为斜线PA与平面α所成角,即为∠PAO,θ2为PA射影AO与α内直线AB所成的角,θ为∠PAB。
其中θ1为斜线PA与平面α所成角,即为∠PAO,θ2为PA射影AO与α内直线AB所成的角,θ为∠PAB。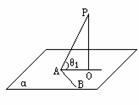 异面直线的距离:除求公垂线段长度外,通常化归为线面距离和面面距离。
异面直线的距离:除求公垂线段长度外,通常化归为线面距离和面面距离。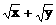 ≤
≤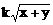 对所有正数x,y都成立,试问k的最小值是多少?
对所有正数x,y都成立,试问k的最小值是多少?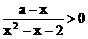
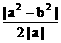 ≥
≥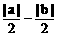
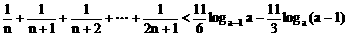 对n∈N+都成立,试求实数a的取值范围。
对n∈N+都成立,试求实数a的取值范围。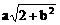 的最值。
的最值。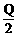 件,问每批进货量Q为多大时,整个费用最省?
件,问每批进货量Q为多大时,整个费用最省?