18.(本小题13分)
解法一:
(Ⅰ)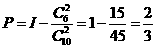 ,即该顾客中奖的概率为
,即该顾客中奖的概率为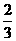 .
.
(Ⅱ)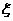 的所有可能值为:0,10,20,50,60(元).且
的所有可能值为:0,10,20,50,60(元).且
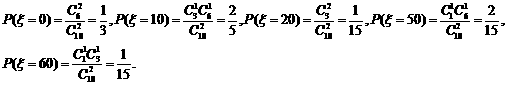
故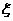 有分布列:
有分布列:
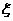 |
0 |
10 |
20 |
50 |
60 |
|
P |
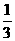 |
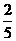 |
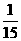 |
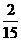 |
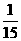 |
从而期望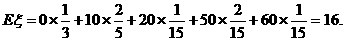
解法二:
(Ⅰ)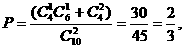
(Ⅱ)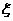 的分布列求法同解法一
的分布列求法同解法一
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值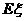 =2×8=16(元).
=2×8=16(元).
21.(山东)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为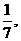 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用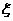 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中所有的白球的个数;
(II)求随机变量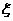 的概率分布;
的概率分布;
(III)求甲取到白球的概率.
解:(I)设袋中原有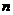 个白球,由题意知
个白球,由题意知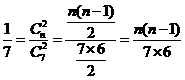
可得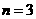 或
或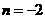 (舍去)即袋中原有3个白球.
(舍去)即袋中原有3个白球.
(II)由题意,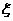 的可能取值为1,2,3,4,5
的可能取值为1,2,3,4,5
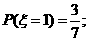
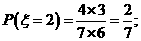
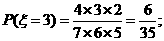
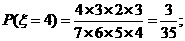
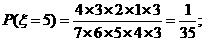
所以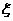 的分布列为:
的分布列为:
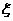 |
1 |
2 |
3 |
4 |
5 |
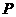 |
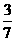 |
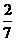 |
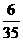 |
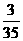 |
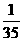 |
(III)因为甲先取,所以甲只有可能在第一次,第三次和第5次取球,记”甲取到白球”为事件 ,则
,则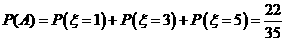
19.(浙江卷)袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是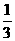 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.(i)求恰好摸5次停止的概率;(ii)记5次之内(含5次)摸到红球的次数为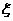 ,求随机变量
,求随机变量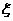 的分布率及数学期望E
的分布率及数学期望E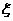 .
.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是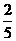 ,求p的值.
,求p的值.
解:(I) (i) 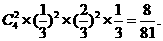
(ii) 随机变量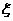 的取值为0, 1, 2, 3.
的取值为0, 1, 2, 3.
由n次独立重复试验概率公式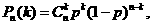 得
得
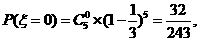
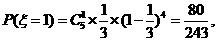
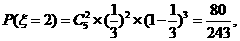
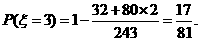
随机变量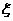 的分布列是
的分布列是
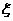 |
0 |
1 |
2 |
3 |
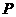 |
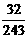 |
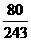 |
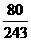 |
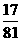 |
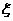 的数学期望是
的数学期望是
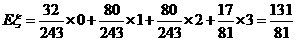
(II) 设袋子A有m个球,则袋子B中有2m个球。
由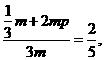
得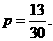
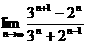 =_3 _________。
=_3 _________。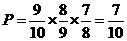 ;
;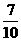 ,由独立重复试验的概率公式得:
,由独立重复试验的概率公式得: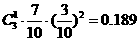 ,
,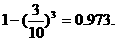
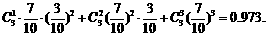
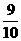 、
、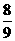 、
、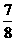 ,且各道工序互不影响。
,且各道工序互不影响。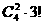 (从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有
(从4个部门中任选2个作为1组,另外2个部门各作为1组,共3组,共有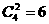 种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为
种分法,每组选择不同的景区,共有3!种选法),记“3个景区都有部门选择”为事件A1,那么事件A1的概率为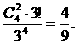
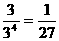 ,事件A2的概率为
,事件A2的概率为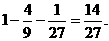
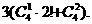 (先从3个景区任意选定2个,共有
(先从3个景区任意选定2个,共有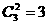 种选法,再让4个部门来选择这2个景区,分两种情况:第一种情况,从4个部门中任取1个作为1组,另外3个部门作为1组,共2组,每组选择2个不同的景区,共有
种选法,再让4个部门来选择这2个景区,分两种情况:第一种情况,从4个部门中任取1个作为1组,另外3个部门作为1组,共2组,每组选择2个不同的景区,共有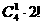 种不同选法.第二种情况,从4个部门中任选2个部门到1个景区,另外2个部门在另1个景区,共有
种不同选法.第二种情况,从4个部门中任选2个部门到1个景区,另外2个部门在另1个景区,共有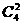 种不同选法).所以P(A2)=
种不同选法).所以P(A2)=